Integral Teilfläche Funktion Rechteck

Question

Aufgabe:

Ein Rechteck mit den Eckpunkten: A=(2/0; B=(6/0); C=(2/5) und D=(6/5) wird durch den Graphen der Funktion : f(x)= x^2 -8x+17 in zwei Teilflächen unterteilt. Berechnen Sie das Verhältnis der beiden Teilfächen.

Problem/Ansatz:

Habe bei dem Rechteck 20 und bei der Funktion 28/3 raus.

Comments

Rechteck = 20 = 60 /3
unterhalb der Funktion = 28 / 3
Oberhalb der Funktion = 32 / 3

28 / 3 zu 32 /3
28 / 32
7 / 8

Answer 1

f(x) = x^2 - 8x + 17x

Da kann etwas nicht stimmen. Schau nochmal genau hin.

A=(2/0; B=(6/0); C=(2/5) und D=(6/5)

Das wäre ein überschlagenes Viereck. Man man man...

Der Lehrer hatte beim stellen der Aufgabe keinen guten Tag.

Nehmen wir das mal so hin

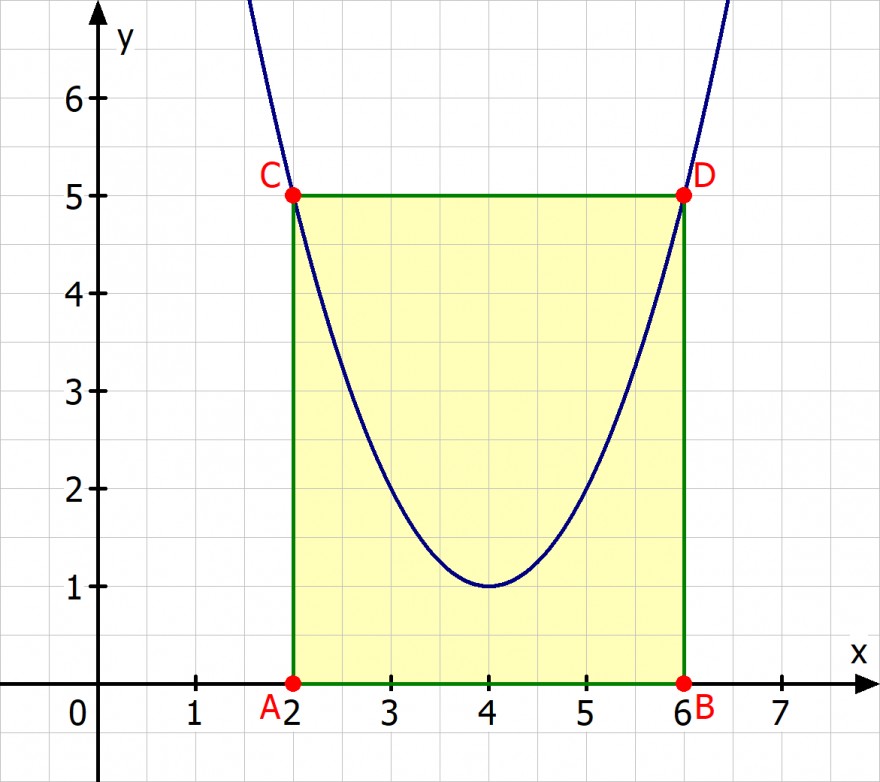
A = 4 * 5 = 20
A1 = 2/3 * 4 * 4 = 32/3
A2 = 20 - 32/3 = 28/3

A1/A2 = (32/3) / (28/3) = 32/28

Comments

Bei der Funktion haben Sie recht. Die lautet x^2 -8x +17. Das Viereck habe ich allerdings richtig abgeschrieben.

---

Dann sind deine 2 Flächen schon richtig. Dann brauchst du doch nur noch die Differenz bilden um die zweite Teilfläche zu bekommen und dann den Quotienten bilden.

---

In der vorletzten Zeile muss es 28/3 statt 28/8 heißen.

---

In der vorletzten Zeile muss es 28/3 statt 28/8 heißen.

Danke für die Bemerkung des Tippfehlers. Ich hatte ja mit dem richtigen Wert weitergerechnet. Insofern war das ja nicht ganz so dramatisch.

---

Gut vom Prinzip her habe ich ja verstanden was ich machen muss. Rechteck gleich 4*5 logischerweise = 20

Dann Aufleiten = 1/3 x^3 -4*x^2 +17x

Dann Integral im Bereich von 2 bis 6 der aufgeleiteten Funktion oder? Das Problem ist, dass das eine hilfsmittelfreie Aufgabe sein soll und ich zu blöd bin, Brüche auszurechnen. Als Ergebnis mit dem Taschenrechner habe ich eine unlogische Zahl raus, die nicht im Verhätnis steht: 58,667. Welche Ergebnisse habt ihr raus?

---

Ok ich habe jetzt 28/3 ohne Taschenrechner raus, habs verstanden danke.

---

Beachte das du als Lösung das Verhältnis der Teilflächen angeben sollst also z.B.

A1/A2 = (32/3) / (28/3) = 32/28

---

Hallo coach,
ist die Lage der Eckpunkte eigentlich
genormt ?
Falls nicht ist die Angabe der Eckpunkte
doch ok.