Rechteck ABCD wird durch den Graphen in zwei Teilflächen zerlegt. Berechne den Flächeninhalt der oberen Teilfläche.

Question

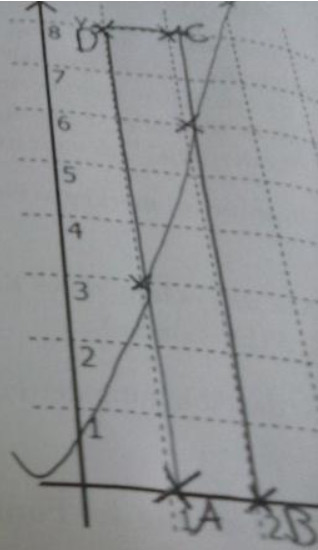
Das Rechteck \( A B C D \) mit \( A(1 \mid 0), B(2 \mid 0), C(2 \mid 8) \) und \( D(1 \mid 8) \) wird durch den Graphen der Funktion f mit \( f(x)=x^{3}, x \in \mathbb{A} \), in zwei Teilflächen zerlegt.

1.1 Skizzieren Sie die beiden Teilfächen in nebenstehendem Koordinatensystem.

1.2 Ermitteln Sie den Flächaninhalt der oberen Teilfläche.

Wie berechne ich den Flächeninhalt?

Answer 1

Fläche im Intervall [1,2] zwischen der Gerade y=8 und der Funktion y=x^3

$$\int_1^2 (8-x^3)dx=\left[8x-\frac{1}{4}x^4 \right]_1^2=(16-4)-(8-\frac{1}{4})=4+\frac{1}{4}=\frac{17}{4}$$

Answer 2

Hi,

Du kannst die untere Teilfläche berechnen.

Diese ist

 

$$A_{\text{int}}=\int_1^2 x^3 = 3,75$$

Nun A_gesucht =  A_Rechteck - A_int = 8-3,75 = 4,25

 

Grüße

Comments

danke, wir sollen aber die obere Teilfläche bestimmen, wie geht das ?

---

Wurde doch gemacht ;).

A_int ist die untere Teilfläche. Folglich ist die obere Teilfläche A_gesucht eben Rechteck A_Rechteck minus untere Teilfläche A_int