ich bekomme es mit meinem Grafikprogramm nicht hin, aber vielleicht hilft Dir auch das:
Die Summe der Winkel in einem Dreieck beträgt 180°, hier also
α = 30°
β = 180° - α - γ = 60°
γ = 90°
Ein Dreieck dieser Form kannst Du leicht konstruieren, indem Du zwei beliebige Punkte A und B nimmst und diese miteinander verbindest, und dann α und β abträgst; der Schnittpunkt dieser beiden neuen Geraden ist dann der Punkt C des Dreiecks.
Der Schnittpunkt der Mittelsenkrechten der Seiten a, b und c ist der Mittelpunkt des Umkreises.
Um diesen schlägst Du jetzt einen Kreis mit dem Radius 3,8 cm.
Dann kannst Du die Seite c mit den Endpunkten A und B so verlängern oder verkürzen, dass die Punkte A und B auf dem Kreisrand liegen. Wieder α und β abtragen und so den Punkt C ermitteln.
In dieser Zeichnung, deren Winkel nicht der Aufgabenstellung entsprechen, habe ich zuerst A, B und C eingetragen, dann den Umkreismittelpunkt D, und schließlich den großen Umkreis.
Das vergrößerte Dreieck hat dann die Eckpunkte F, G und H statt A, B und C:
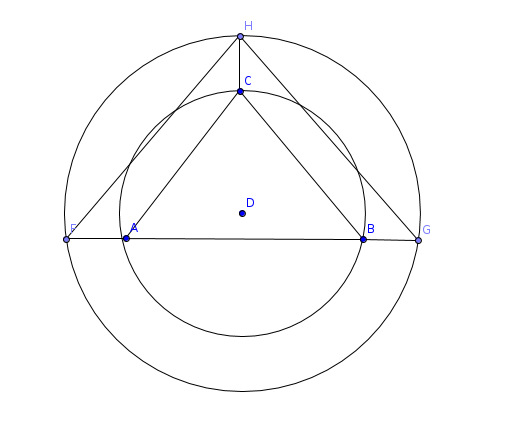
Nicht sonderlich elegant, aber es müsste so klappen.
Besten Gruß