Potenz- Polynomfunktionen Graphen

Question

Aufgabe:

Skizziere jeweils den Funktionsgraphen, ohne eine Wertetabelle zu erstellen. Beschreibe deine Überlegungen. Überprüfe deine Zeichnung mithilfe von Technologieeinsatz.

a.) y= x² + 5

b.) y= (x+5)²

c.) y= (x-4)² + 3

Problem/Ansatz:

Wir haben heute in Mathe ein neues Thema begonnen und da mussten wir diese Aufgabe in der Schule lösen. Ich bin gar nicht mitgekommen. Ich verstehe es nicht und der Lehrer hat es auch sehr kompliziert erklärt. Kann es mir bitte jemand erklären? ( Wenn möglich mit Skizze und Rechenschritte um es zu verstehen )

Answer 1

Eine Parabel der Form $$y = (x-a)^2 + b$$ ist nach oben geöffnet, weil der Faktor vor der Klammer größer Null ist, hier ist er 1. Der kleinste Wert wird angenommen, wenn die Klammer $(x-a)^2$ am kleinsten wird. Das ist dert Fall für $x = a$.

Also hat die Parabel ein Minimum für $x = a$. Denn da wird die Klammer 0. Kleiner kann sie nicht werden, da ein Quadratzahl immer größer gleich Null ist.

Nullstellen können nur für $b \le 0$ auftreten, da ansonsten zwei positive Zahlen addiert werden, und das kann niemals NUll werden.

Als Beispiel ist bei Dir im Fall (c)

$a = 4$ und $b = 3$.

D.h. das Minimum liegt bei $x = 4$ und Nullstellen gibt es nicht.

Comments

Vielen Dank!

Answer 2

y= x² + 5

Das x² ist nie negativ, sondern für x=0 hat es den Wert 0 und

rechts und links symmetrisch von 0 entstehen immer positive Werte,

die - je weiter sie von 0 entfernt sind - immer größer werden.

Also geht der Graph durch den Punkt (0;5) und rechts und links davon

geht es nach oben. Sieht dann so aus:

Plotlux öffnen

f₁(x) = x²+5Zoom: x(-5…5) y(-1…30)

Comments

Vielen Dank!

Answer 3

Hallo,

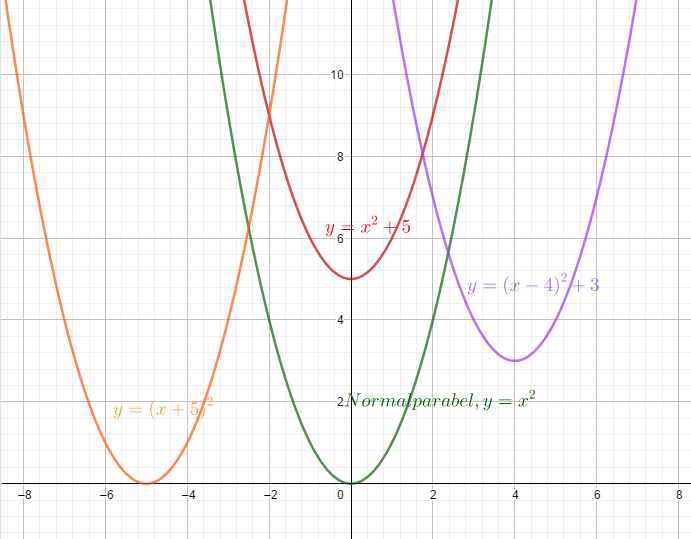
die Funktionsgleichung der Normalparabel lautet $y=x^2$

Wird diese entlang der y-Achse um e Einheiten verschoben, sieht der Funktionsterm einer Parabel so aus:

$y = x^2 + e$

$y = x^2 + 5$ Die Parabel wurde um 5 Einheiten nach oben verschoben.

$y = x^2 - 5$ Die Parabel wurde um 5 Einheiten nach unten verschoben.

Wir die Normalparabel um d Einheiten entlang der x-Achse verschoben, sieht die Funktionsgleichung so aus:

$y=(x+d)^2$

$y=(x+5)^2$ Die Parabel wurde um 5 Einheiten nach links verschoben.

$y=(x-5)^2$ Die Parabel wurde um 5 Einheiten nach rechts verschoben.

Natürlich ist auch eine Kombination aus den Verschiebungen möglich:

$y=(x-4)^2+3$

Verschiebung um 4 Einheiten nach rechts und drei nach oben. Der Scheitelpunkt hat die Koordinaten (4|3)

Gruß, Silvia

Comments

Vielen Dank!

Answer 4

Alle angegebenen Parabeln sind nach oben offen und haben die Form der

$$Normalparabel; y=x^2$$$$Scheitelpunkt→S(0;0)$$

a.)

$$y= x^2 + 5$$$$x= 0 → y=0^2+5=5$$$$Scheitelpunkt→S(0;5)$$
Es gibt keine Klammer und kein x sondern nur ein x^2 also liegt der Scheitelpunkt bei x=0

b.)

$$y= (x+5)^2$$$$(x+5)=0→x=-5$$$$→y=0^2+0=0$$$$Scheitelpunkt→S(-5;0)$$

Der Wert in der Klammer wird 0, wenn x= -5

Es gibt keine Konstante

c.)

$$y= (x-4)^2 + 3$$$$(x-4)=0→ x=4$$$$→y=0^2+3=3$$$$Scheitelpunkt→S(4;3)$$

In der Klammer 0 wenn x =4 Konstante = 3