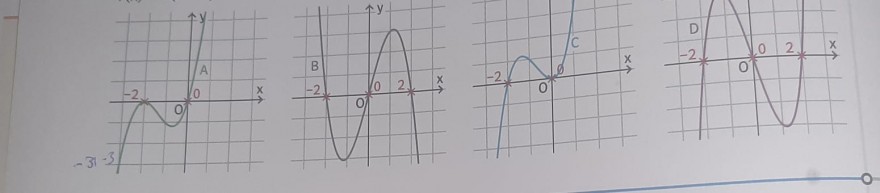Linearfaktordarstellung - Funktion und ihre Graphen

Question

Aufgabe:

Ordnen Sie jeder Funktion den passenden Graphen zu.

f(x) = x(x+2)²; g(x) = x(x-2)(x+2); h(x) = -x(x-2)(x+2); i(x) = x²(x + 2)

Problem/Ansatz:

Die Nullstellen der Funktion g(x) betragen x₁ = 0; x₂ = 2 und x₃ = - 2

Daraus folgen zwei Möglichkeiten Graph B und Graph D, deshab führt man eine Punktprobe um die Funktion zu bestimmen:

Vom Graph B: Punkt P(-1|-3), demnach setze Ich diesen Punkt in die Funktion von g(x) ein:

      g(-1) = -1(-1 -2)*(-1 + 2)

<=>g(-1) =  -1 * (-3) * 1 = 3

Ich sehe aber nirgendwo in meinen Graphen, dass da ein Punkt (-1|9) vorhanden ist, demnach probiere Ich es mit den Graphen von D aus.

Vom Graph D: Punkt P(-1|3), demnach setze Ich diesen Punkt in die Funktion von g(x) ein:

       g(-1) = 1(-1 -2)*(-1 + 2)

<=> g(.1) = -1 * (-3) * 1 = 3

=> Somit ist die Funktion von g(x) zu dem Graphen von D zugeordnet.

-------------------------------------------------------------------------------------------------------------------------------------------------------------------

Die Nullstellen der Funktion f(x) betragen x₁ = 0; x₂ = -2

Daraus folgen zwei Möglichkeiten Graph A und Graph C, deshab führt man eine Punktprobe um die Funktion zu bestimmen:

Vom Graph A: Punkt P(-1-1), demnach setze Ich diesen Punkt in die Funktion von f(x) ein:

f(-1) = -1(-1+2)² = -1

=> Somit ist die Funktion von f(x) zu dem Graphen von A zugeordnet.

--------------------------------------------------------------------------------------------------------------------------------------------------------------------

Die Nullstellen der Funktion h(x) betragen x₁ = 0; x₂ = 2 und x₃ = - 2

=> Somit ist die Funktion von h(x) zu dem Graphen von B zugeordnet.

----------------------------------------------------------------------------------------------------------------------------------------------------------------------

Die Nullstellen der Funktion i(x) betragen x₁ = 0; x₂ = - 2

=> Somit ist die Funktion von i(x) zu dem Graphen von C zugeordnet.

----------------------------------------------------------------------------------------------------------------------------------------------------------------------

Answer 1

f(x) = x(x+2)²; g(x) = x(x-2)(x+2); h(x) = -x(x-2)(x+2); i(x) = x²(x + 2)

f hat eine einfache Nullstelle bei 0 und eine doppelte Nullstelle bei -2. Damit kommt nur Graph A infrage

i hat eine doppelte Nullstelle bei 0 und eine einfache Nullstelle bei -2. Damit kommt nur C infrage

g hat einen positiven Leitkoeffizent nach dem ausmultiplizieren und damit kommt nur Graph D infrage.

h muss also zum Graphen von B gehören.

Hier musst du eigentlich nichts rechnen. sondern nur schauen.