Erwartungswert beim Kugelnziehen berechnen

Question

Es werden 2 Kugeln gezogen. die Augensumme wird ausgezahlt.

Zufallsgröße X=Auszahlung

geben Sie den Erwartungswert von X an.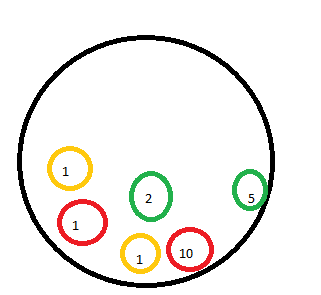

Also ich habe mir erstmal Gedanken darüber gemacht, was die Kombinationen sein könnten

Man könnte 3x 1,1 haben - Summe 2(3mal)

1,2 oder 2,1 - Summe 3

2,5 oder 5,2 - Summe 7

1.5 oder 5,1 -Summe 6

10.1 oder 1.10 - Summe 11

10,2 oder 2,10 - Summe 12

10,5 oder 5,10 - Summe 15

Xi	p(x=x)
2	3/15
3	2/15
7	2/15
6	2/15
11	2/15
12	2/15
15	2/15

Als Erwartungswert hätte ich dann 7.6.

Stimmt es?

Answer 1

Wenn ich mich nicht verrechnet habe, dann so: $$\begin{array}{r|r|r|r|r|r|r|r|} \text{Auszahlung } x_i & 2 & 3 & 6 & 7 & 11 & 12 &15 \\ \hline P(X = x_i) & 0.2 & 0.2 &0.2 & \frac{1}{15} & 0.2 & \frac{1}{15}  & \frac{1}{15}\end{array}$$ wobei $$P(X=2)=\frac{3}{6}\cdot \frac{2}{5}=\frac{1}{5}$$$$P(X=3)=\frac{3}{6}\cdot \frac{1}{5}+\frac{1}{6} \cdot \frac{3}{5}=\frac{1}{5} $$$$P(X=6)=\frac{1}{6}\cdot \frac{3}{5}+\frac{3}{6}\cdot \frac{1}{5}=\frac{1}{5}$$$$P(X=7)=\frac{1}{6}\cdot \frac{1}{5}\cdot 2=\frac{1}{15}$$$$P(X=11)=\frac{1}{6}\cdot \frac{3}{5}+\frac{3}{6}\cdot \frac{1}{5}=\frac{1}{5}$$$$P(X=12)=\frac{1}{6}\cdot \frac{1}{5}\cdot 2=\frac{1}{15}$$$$P(X=15)=\frac{1}{6}\cdot \frac{1}{5}\cdot 2=\frac{1}{15}$$ Dann gilt:$$\mu_{X} = \mathrm{E}(X) = \sum_i x_i \cdot P(X = x_i)=\frac{20}{3}=6.\bar{6}$$

Comments

Können Sie mir vielleicht sagen, was für Kombinationen sie genommen haben? damit ich besser nachvollziehen kann, woher die Zahlen kommen :) z.b 1 gelb 1rot / die rote 10 und die rote 1/ etc

---

In der Urne liegen 6 Kugeln und ein Auszahlungswert von 20.
Bei zweimaligem Ziehen ist der Erwartungswert also 2·(20/6) = 20/3

---

Können Sie mir vielleicht sagen, was für Kombinationen sie genommen haben? damit ich besser nachvollziehen kann, woher die Zahlen kommen :) z.b 1 gelb 1rot / die rote 10 und die rote 1/ etc

Du hast doch die möglichen Auszahlungssummen alle feinsäuberlich notiert.

\(P(X=2)\) bedeutet, dass ich nach der Wahrscheinlichkeit suche, dass 2 ausgezahlt wird, also die Summe der gezogenen Kugeln gleich 2 ist.

Das geht nur mit einem Pfad, nämlich 1 und dann wieder 1.

3/6*2/5

Das geht analog so weiter.

---

In der Urne liegen 6 Kugeln und ein Auszahlungswert von 20.
Bei zweimaligem Ziehen ist der Erwartungswert also 2·(20/6) = 20/3

Ja, im (arithmetischen) Mittel erhält man pro Zug (10+5+2+1+1+1)/6=20/6. Somit spart man sich die ganzen Pfadwahrscheinlichkeiten.

---

Achso also die Kombinationen waren richtig, nur die Wahrscheinlichkeiten nicht

Danke :)