Ein pythagoreisches Zahlentripel besteht aus den natürlichen Zahlen a, b und c mit der Eigenschaft a2+b2=c2. Das kleinste und bekannteste Beispiel ist (3,4,5) mit 32+42=52. Euklid hat in Band IX seiner Enzyklopädie zeitgenössischen, mathematischen Wissens eine Methode genannt, mit der man alle pythagoreischen Tripel finden kann. Diese Methode ist nicht für alle Schülerinnen und Schüler leicht nachvollziehbar. Heinz Klaus Strick (Heinz Klaus Strick, Mathematik ist schön, ISBN 978-3-662-59059-1) zeigt einen sehr anschaulichen Weg auf dem Schülerinnen und erste Tripel leicht finden: Ergänzt man ein Quadrat (hier gelb) nach rechts und unten durch einen sogenannten ‚Winkelhaken‘ (hier rot),
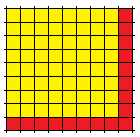
so entsteht ein neues Quadrat. Wenn das Ausgangsquadrat n×n Felder hat, so hat der Winkelhaken 2·n+1 Felder. 2·n+1 ist für natürliche Zahlen n>1 eine ungerade Zahl und selbstverständlich gilt n2+(2n+1)=(n+1)2. Wenn 2n+1 eine Quadratzahl ist, dann ist ein pythagoreisches Zahlentripel gefunden.
Die ungeraden Quadratzahlen >1 sind 32=9, 42=16, 52=25, 62=36 und so weiter. Wenn eine ungerade Quadratzahl (2n+1)2 die Anzahl der Felder eines Winkelhakens ist, findet man leicht das zugehörige kleinere Quadrat mit n2 Feldern, welches der Winkelhaken zu einem größeren Quadrat ergänzt. Ein Beispiel:
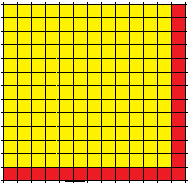
Ein Winkelhaken mit 2·12+1=52 Feldern ergänzt das 12·12-Quadrat zum 13×13-Quadrat. Folglich gilt 122+52=132 und ein neues pythagoreisches Zahlentripel (12, 5, 13) ist gefunden. Man braucht also nur von einer ungeraden Quadratzahl (hier 52=25) auf die Seitenlänge des kleineren Quadrats (hier (25-1)/2=12) zu schließen, um ein pythagoreisches Zahlentripel zu erhalten.
Etwas Entsprechendes funktioniert auch für das Anfügen zweier Winkelhaken an ein kleineres Quadrat:
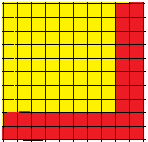
Hier sind zunächst zwei aufeinanderfolgende ungerade Zahlen zu bestimmen, deren Summe eine Quadratzahl ist (im Beispiel 17+19=62). Die um 1 verminderte kleinere der beiden ungeraden Zahlen wird halbiert ( hier (17-1)/2=8) und so die Seitenlänge des kleineren Quadrats gewonnen. Da n2+(2n+1)+(2n+3)=(n+2)2 wird ein pythagoreisches Tripel (hier 8,6,10) gefunden, nachdem zwei aufeinanderfolgende ungerade Zahlen gefunden wurden, deren Summe eine Quadratzahl ist. Die Folge der Summen zweier aufeinanderfolgender ungerader Zahlen lautet: 4, 8, 12, 16, 20, 24, 28, 32, 36, ….. Darin sind 4, 16, 36, 64, … genau die durch 4 teilbaren Quadratzahlen.
Konstruieren wir exemplarisch nun ein pythagoreisches Tripel zu 16=7+9. Dann ist (7-1)/2=3 und 32+42=(3+2)2. Das ist das bereits das genannte Tripel (3,4,5). Das zuvor gefundene Tripel (6,8,10) ist übrigens genau das Doppelt davon. Ein pythagoreisches Tripel, das nicht Vielfaches eines anderen pythagoreischen Tripels ist, heißt ‚primitives‘ pythagoreisches Tripel. Auf der Grundlage von 31+33=64 kann durch das Anfügen zweier Winkelhaken an das 15×15-Quadat das primitive Tripel (15,8,17) gefunden werden.
Betrachtet man pythagoreische Dreiecke, die beim Anfügen von 3 Winkelhaken entstehen, stellt man fest, dass keine neuen primitiven Tripel gefunden werden.
Die hier vorgeschlagene Konstruktion geht zurück auf den Satz: Die Summe der ersten n ungeraden Zahlen ist n2.
Dieser Satz kann anschaulich erhärtet werden, indem man ein gleichseitiges Dreieck in n Zeilen kleiner gleichseitiger Dreiecke zerlegt und diese gelb und rot einfärbt, wobei gleiche Farben sich nur in Eckpunkten berühren:
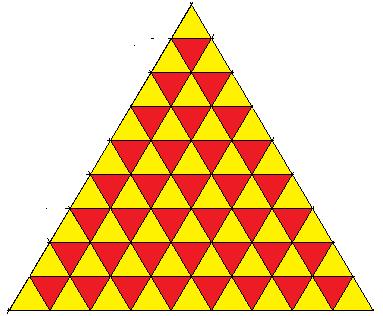
In jeder Zeile erkennt man eine ungerade Zahl von Dreiecken. Da eine Zerlegung in n Zeilen (hier n=9) vorliegen soll, ist die Gesamtzahl der kleinen gleichseitigen Dreiecke gleich der Summe der ersten n ungeraden Zahlen. Die Anzahl der gelben Dreiecke ist gleich der Summe der ersten n natürlichen Zahlen und berechnet sich als n(n+1)/2. Die Anzahl der roten Dreiecke ist gleich der Summe der ersten n-1 natürlichen Zahlen und berechnet sich als (n-1)n/2.
Wie man leicht nachrechnen kann, gilt n(n+1)/2+(n-1)n/2 = n2.