Hallo,
wenn du die Funktionen gleichsetzt, erhältst du die Schnittpunkte.
Du sollst aber herausfinden, für welchen Punkt y = -x die Tangente ist.
Dazu musst du erst einmal die Punkte bestimmen, die die gleiche Steigung wie die Gerade, also -1 haben:
$$f(x)=x^3-6x^2+8x\\f'(x)=3x^2-12x+8\\3x^2-6x^2+8x=-1\\ x^2-4x+3=0\\x_1=1\quad x_2=3\\ P(1|3)\quad Q(3|-3)$$
Setze jetzt die Koordinaten der Punkte in die allgemeine Geradengleichung y = mx + b ein, um b zu bestimmen:
3 = -1 · 1 + b ⇒ b = 4
Tangentengleichung y = -x + 4, also kommt P nicht in Frage
-3 = -1 · 3 + b ⇒ b = 0
Tangentengleichung y = -x
Also ist die gesuchte Stelle x = 3
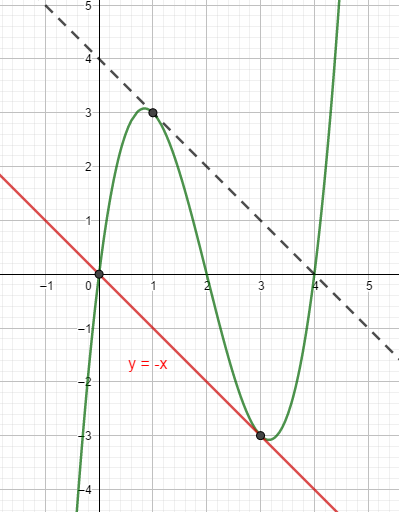
Gruß, Silvia