Das symmetrische Trapez, mit gegebenen Grundlinien und einem Winkelverhältnis.

Question

Das symmetrische Trapez hat die Grundlinie a = 20cm und b = 13cm. Ausserdem ist der Winkel α = ∠(BAD) dreimal so gross wie der Winkel ∠(BAC). Berechnen Sie α.

Lösung: α = 59.6°

 

Hat jemand einen guten Lösungsweg?

Vielen Dank

Reto

Comments

So bin nun doch auf eine Lösung gekommen:

Habe Winkel β so gewählt...

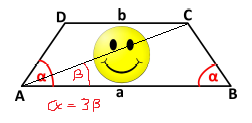
...und eine Gleichung über die Höhe aufgestellt.

geg: α = 3β , a = 20cm , b = 13cm

ges: α

Gleichung:

(a-b)/2*tan(3β) = (a+b)/2*tan(β)    d.h.    3.5tan(3β) = 16.5tan(β)

Formelbuch: tan(3β) = [3tan(β)-tan3(β)]/[1-3tan2(β)]

3.5*[3tan(β)-tan³(β)]/[1-3tan²(β)] = 16.5tan(β)
                    3.5*tan(β)*[3-tan²(β)] = 16.5*tan(β)*[1-3tan²(β)]
                              10.5-3.5tan²(β) = 16.5-49.5tan²(β)
                                        46tan²(β) = 6
                                            tan²(β) = 6/46
                                              tan(β) = (6/46)^1/2
                                                      β = arctan[(6/46)^1/2]
                                                      β = 19.858°

                                                      α = 3β = 59.6°

Answer 1

Irgendwie ist die Aufgabe  verwirrend , ein symmetrisches Trapez ist ein gleichschenkliges Trapez und die beiden Basiswinkel sind gleich.

die Winkelinnensumme ist  360°

hier bedeutet es :

2α +2γ= 360°

und α = 3γ          Einsetzungverfahren wählen

2(3γ) +2γ= 360°

          8γ= 360°           γ= 45°

                                    α=135°

Comments

γ ist nicht gegeben. Den beschriebenen Winkel habe ich jetzt einmal mit β bezeichnet.

Danke für deine Mühe!

Answer 2

Hi,

ich würde da wohl so rangehen:

(Da es ein symmetrisches Trapez ist, muss sowohl rechts als auch links der "Überhang" der Basis gleich groß sein, also 20-13 = 7 -> 7/2 = 3,5)

 

Nun ein Gleichungssystem aufstellen:

x/3,5 = tan(y)

x/16,5 = tan(y/3)

Nach x auflösen und gleichsetzen:

3,5tan(y) = 16,5tan(y/3)

 

Das hab ich nun in den TR gehauen:

y = 59,6°

 

Grüße

Comments

Ich habe die gleich Gleichung über die Höhe aufgestellt, konnte sie dann einfach nicht schriftlich auflösen. Das Oberthema sind Trigonometrische-Gleichungen und einen Taschenrechner mit solve-Funktion ist uns leider auch nicht erlaubt.
Wenn du immer noch Lust hast und mir die Auflösung machen kannst, währe ich dir unendlich dankbar! :)

PS: Habe übrigens mit α = 3β und β gearbeitet, da tan(3β) besser zu bearbeiten ist als tan(α/3)!

---

Dein PS ist völlig in Ordnung :).

Hmm, hatte vorher auf die Schnelle nicht gesehen, wie man das handschriftlich löst, aber über den TR zumindest das Ergebnis bestätigen lassen. Komme aber auch bei längeren anschauen nicht auf eine sinnvolle Möglichkeit das von Hand zu lösen.

Sehe auch keine andere Herangehensweise :/.

P.S.: Gerade spaßeshalber mit dem Sinussatz gemacht. Komme am Ende wieder auf trigonometrische Gleichungen, wo es nen TR bräuchte...