gleichseitiges Dreieck, Seckseck Gitterpunkte

Question

Aufgabe:

Wie viele Gitterpunkte enthält ein gleichseitiges Dreieck (ein reguläres Seckseck - Rand und Innen), dessen eine Seite eine Gitterstrecke der Länge n ist?

Problem/Ansatz:

Ich komm hier nicht so ganz weiter.

Gleichseitiges Dreieck:

Hier hab ich einmal, dass der Rand 3*n hat. Aber wie stelle ich jetzt eine Formel auf, wo auch das Innere berücksichtigt wird?

Regulären Sechseck:

Hier hab ich auch nur der Rand, der 6*n ist, weils ja 6 Seiten sind, aber gehts hier für innen eig.? Hab jz schon ein paar Skizzen angefertigt aber komm leida nicht weita.

Comments

Wie ist denn das mit dem 'Gitter' gemeint. Ist es ein rechtwinkliges Gitter, was keinen unmittelbaren Bezug zu dem Dreieck oder Sechseck hat - so wie auf dem Bild in Rolands Antwort, oder ist es vielmehr ein Gitter wie hier abgebildet:

???

Bei der Länge einer Dreiecksseite von z.B. \(4n\) wären das \(15\) Gitterpunkte.

---

Es stehen leider nicht mehr Angabe, aber im Löser steht die Lösung, die lautet ((n+1)*(n+2))/2 vl kannst du daran erkennen, was gemeint ist, ich leider nicht, denn ich vesteh die Formel nicht so ganz.

---

$$ \sum\limits_{k=1}^{n+1}{(k} =(n+1)(n+2)/2$$

$$n=4→15 Gitterpunkte$$

Wie von Werner beschrieben.

---

Für einen Studenten wirken verunstaltete Wörter wie "jz", "leida" und "weita" schon etwas seltsam.

:-)

---

Haha das tut mir leid, aber wenn ich so schreibe, dann rutsch ich meistens in die Mundart, ich werd sehn, dass ich das wegbekomm und bin ja erst im ersten Semester :-)

Answer 1

Das kommt ganz auf die Lage von Sechseckrand und Gitterlinien zueinander an. Eine Möglichkeit für das Sechseck wäre:

Die Gitterlinien schneiden sich in 11 Punkten innerhalb der Sechsecks.

Comments

Okay ds bedeutet, innerhalb ist es abhängig von der Lage, aber der Rand stimmt das das hier immer die Formel 6*n gilt nein oda?

Answer 2

Hallo Mathe-Student,

Löser steht die Lösung, die lautet ((n+1)*(n+2))/2 vl kannst du daran erkennen, was gemeint ist,

Ja - kann ich. Das sind die sogenannten Dreieckszahlen. Nur mit dem kleinen Unterschied, dass \(n\) bei Dir die Länge einer Seite ist. Normalerweise ist \(n\) die Anzahl der Punkte auf einer Seite. Setze in die Berechnung für das \(n\) dort \(n+1\) ein, so bekommst Du die identische Formel.

... denn ich vesteh die Formel nicht so ganz.

Nun 'verstehen' solltest Du die Formel schon! \(n\) ist dort die 'Länge' einer Seite in 'Gitterabständen' gemessen. Oben in dem Bild aus meinem Kommentar ist \(n=4\). Das macht dann $$\triangle_4 = \frac 12 (4+1)(4+2) = 15$$Gitterpunkte. Wie sie zustande kommt, sollte aus dem WIki-Artikel zu entnehmen sein.

Bei dem Sechseck beginne mit \(n=1\). Das sind die 7 schwarzen Punkte

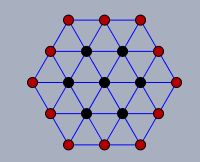
mit jedem weiteren Punkt auf den Seiten kommen \(6n\) Punkte hinzu. Die Folge wäre also$$ 7, \, 19,\, 37,\ 61,\, \text{usw.}$$Kommst Du selber auf die 'Formel' ... sonst öffne den Spoiler

[spoiler]

$$S_n = 3n(n+1) + 1$$

[/spoiler]

Gruß Werner

Comments

Ahh okay das mit der Formel ist mir jetzt klar, ich war eigentlich schon auf einen guten Weg, also hab schon mit einem Rechteck und so gearbeitet, aber kam nicht weiter, dankee.

Aber mit dem Seckseck ds versteh ich nicht. n=1 is 6 n=2 ist 12 und immer so weiter, und mit jedem weiteren Punkt kommen 6*n weitere hinzu is ma auch noch klar und die Formel ist jz für das Innere oder? Die is ma völlig unklar muss i sagen :-(

Wieso 3n?

Ist das n+1 hängt das mit den Exkpunkten zusammen weil wenn n=1 ist hat man im inneren ja n+1?

---

... und die Formel ist jz für das Innere oder? Die is ma völlig unklar muss i sagen :-(

Was heißt 'innere'? Die Formel ist die Antwort auf die Frage, die oben in der Aufgabe steht.

Wie viele Gitterpunkte enthält ein reguläres Seckseck (Rand und Innen), dessen eine Seite eine Gitterstrecke der Länge n ist?

Auf dem Rand liegen \(6n\) Punkte - also kommen mit jeder Vergrößerung der Seite \(6n\) Punkte hinzu. Ein Sechseck mit Seitenlänge \(1\) hat 7 Punkte (nicht 6). Ein Punkt in der Mitte und sechs auf dem Rand ist zusammen 7. Damit bekommt man$$\begin{aligned} S_1 &= 7 \\ S_2 &= 7 + 6 \cdot 2 = 19 \\ S_3 &= 19 + 6 \cdot 3 = 37 \\ S_4 &= 37 + 6 \cdot 4 = 61\end{aligned}$$das nennt man eine arithmetische Folge zweiter Ordnung.
Da sie von '2. Ordnung' ist, kann man sie durch ein Polynom 2.Ordnung beschreiben - also allgemein \(S_n = an^2 +bn + c\). Wobei die Koeffizienten \(a\), \(b\) und \(c\) heraus zu finden sind.
Kennst Du die Folge der Quadratzahlen \(1,4,9,16, ...\)?
Berechne mal die Differenzen zweier auf einander folgender Quadratzahlen. Was fällt Dir auf?

---

Wieso 3n?

\(3n\) (bzw. \(3n^2\)), da die Steigerung von \(S_{n-1}\) nach \(S_n\) immer \(6n\) ist. Vor dem quadratischen Term steht immer die Hälfte des Faktors, mit dem die Differenz multipliziert wird. $$3 = \frac 12 \cdot 6$$ Bei den Quadratzahlen ist die Differenz \(2n-1\). Folglich steht vor dem quadratischen Term der Quadratzahlen \(Q_n\) eine 1. Muss ja auch  \(Q_n = 1 \cdot n^2\)!

---

Ahh danke für die Hilfe. Auf deine Frage: Differenz zwei aufeinander folgender Quadratzahlen: hier ist immer 2 Unterschied, wenn man das ausprobiert. Und bei dem Beispiel sind immer 12 Unterschied.

---

\(7, \, 19,\, 37,\ 61,\, \text{usw.}\)

Ich übersetze das mal.

 1+6

1+6+2*6

1+6+2*6 +3*6

1+6 +2*6+ 3*6 + 4*6

Jetzt fehlt doch nur der Beweis und da kann es doch nur um die inneren Punkte der sechs gleichseitigen Dreiecke gehen.

3*6 =1*12 +1*6

4*6=1*12 +2*6

5*6= 1*12 +3*6

Aussen werden es immer 12 Gitterpunke mehr und innen werden 6* (n+1) Punkte dazu addiert das Ganze wohlformuliert sollte den Beweis ergeben.

Gute Nacht,

Hogar

---

Ok nein, ich kann dem einfach nicht folgen :-(

Ich mein das mit der geometr. Folge zweiter Ordnung das ist mir jetzt schon klar. Aber dein letzter Kommentar, ab "Jetzt fehlt nur noch der Beweis..." meinst du da die 6 gleichseitigen Dreiecke innerhalb, also welche die schwarzen Punkte einbeziehen oda was?

---

Für n=1 hast du

6+1

Gitterpunkte

Bei n = 2 kommen 12 Gitteritter Punkte dazu (6 Gitterpunke außen und 6 Gitterpunkte auf den Verbindungen zur Mitte.

A(1)= 1+6

A(2)=1+6+2*6

Bei n=3 kommen wieder 12 Punkte dazu, zusätzlich aber 6 Punkte innerhalb der 6 Dreiecke I

$$A(3)= A(2)+2*6+1*6= A(2)+3*6$$

$$A(3)= 1+6*\sum\limits_{k=1}^{3}{k} $$

Bei n=4

$$A(4)=A(3)+ 2*6 +2*6$$

$$A(4)= 1+6*\sum\limits_{k=1}^{4}{k} $$

Bei der Länge n

$$A(n)= 1+6*\sum\limits_{k=1}^{n}{k} =$$$$1+6*n*(n+1)/2=$$$$1+3*n*(n+1)$$

---

Achso, diese 6 Dreiecke innerhalb die hab ich irgendwie nicht verstanden, ich glaub jz hab ichs wirklich danke

---

Werner-Salomon war doch so freundlich uns eine Zeichnung zu machen, wenn du dies Dreieck vergrößert, kommen im Inneren 3 Punkte dazu und dann 4 usw.

https://www.mathelounge.de/?qa=blob&qa_blobid=4343901078397467810

---

diese 6 Dreiecke innerhalb die hab ich irgendwie nicht verstanden

ich auch nicht!

---

https://www.mathelounge.de/?qa=blob&qa_blobid=4343901078397467810

und ich dachte, es geht hier um das Sechseck - jetzt bin ich völlig verwirrt!

---

Ich habe ein Sechseck, das sind bei der Länge n=1 6 Gitterpunkte außen und ein Gitterpunkt in der Mitte.

Wenn wir die Punkte außen mit ihren Nachbarn und der Mitte verbinden, bekommen wir 12 Strecken . Wir sehen dann also 6 gleichseitige Dreiecke.

Wenn die Länge un eins erhöht wird, kommen 12 Punkte auf den Strecken dazu. Im Inneren der Dreiecke tut sich noch nichts.

Wenn die Länge wieder um eins erhöht wird, entsteht im Inneren der gleichseitigen Dreiecke zusätzlich ein Gitterpunkt.

Danach kommen innen 2 Punkte dazu.

Das Dreieck von Werner zeigt uns den Fall, dass sich im Inneren drei Gitterpunkte befinden.

Beim nächsten Mal kommen dann 6* 3 im Inneren dazu ( zusätzlich zu den 12 zusätzlichen Punkten auf den genannten Strecken.

https://www.mathelounge.de/?qa=blob&qa_blobid=4343901078397467810

---

Ich bin nicht gut beim Zeichnen.

Text erkannt:

:俞

Answer 3

Gitterpunkte Sechseck mit der Seitenlänge n

$$A(n)=2n+1+2 \sum\limits_{k=n+1}^{2n}{k} =$$$$2n+1+2( \sum\limits_{k=1}^{2n}{k} -\sum\limits_{k=1}^{n}{k})=$$$$2n+1+2n*(2n+1)-n(n+1)=$$$$4n^2+4n+1-n^2-n=$$$$3n(n+1)+1$$

Gitterpunkte Dreieck mit der Seitenlänge n

$$A(n)= \sum\limits_{k=1}^{n+1}{k} =$$$$(n+1)(n+2)/2$$