Hallo zusammen,
ich habe hier folgende bei Aufgabe, bei der ich nicht ganz weiter komme:

Text erkannt:
Sei \( P \) ein Punkt innerhalb eines Quadrats \( A B C D \), sodass \( P A B \) ein gleichschenkliges Dreieck ist, dessen Basiswinkel bei \( A \) und \( B \) liegen und jeweils \( 15^{\circ} \) betragen. Zeigen Sie, dass \( P C D \) ein gleichseitiges Dreieck ist.
Ich habe versucht mir die Aussage erstmal Beispielhaft klarzumachen. Dafür habe ich mir das Ganze mal exemplarisch in GeoGebra zeichnen lassen (Zeichnung minimal ungenau (Der Winkel BPA sollten 150° sein)):
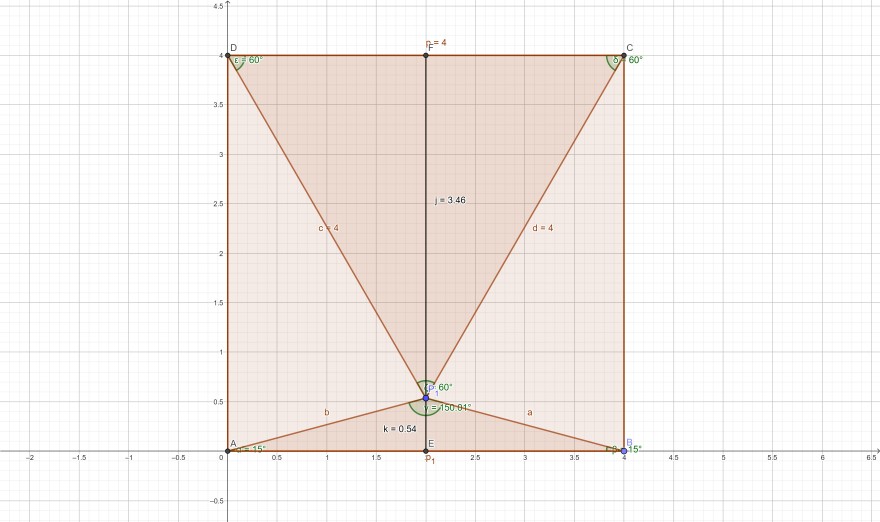
https://www.geogebra.org/classic/fykd7znu
Nach Voraussetzung habe ich ein gleichschenkliges Dreieck, das heißt der Punkt E ist Mittelpunkt der Strecke AB, genauso wie F Mittelpunkt von CD ist, wobei \(|AB|=|CD| \). Jetzt habe ich versucht irgendwie an die Höhe EP zu kommen, z.B. durch: \( \sin(15°) \cdot AP = EP \). Problematisch dabei ist natürlich, dass mir das Wissen über AP fehlt.
Wirklich hilfreiche Sätze in der Vorlesung finde ich auch nicht. Kann mir vielleicht jemand einen Hinweis geben, wie ich weitermachen könnte?