R3 Matrix Rotation y-z-ebene Winkel

Question

Aufgabe

Wie groß muss der Drehwinkel φ (in Grad und −90∘≤φ≤90∘ ) einer Rotation im R3 um die y -Achse sein, damit das Bild des dreidimensionalen Vektors u⃗ =(−1,−8,−4)T in der y−z-Ebene liegt.
Numerische Eingabe in Grad, Genauigkeit mit 1 Stelle gerundet nach dem Komma.

Problem/Ansatz:

Habe leider nicht den Hauch einer Ahnung wie ich das Moped angehen soll... Wäre für Hilfe und einen nachvollziehbaren Rechenweg echt dankbar :/

Answer 1

Hallo,

mache Dir ein Bild:

(klick auf das Bild und rotiere die Szene mit der Maus)

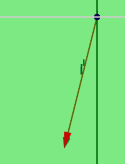
wie weit muss man den roten Vektor im Bild mit den Koordinaten \((-1|\, -4)\) um den Punkt \(Y\) drehen, damit er mit der schwarzen Geraden zur Deckung kommt? Und in welche Richtung dreht man, wenn man von hinten auf die Y-Achse schaut?

$$\varphi = -\arctan \left( \frac14\right) \approx -14,0°$$

Comments

vielen Dank für diese eindeutige Darlegung, habs denke ich geblickt :D

Answer 2

\( \left(\begin{array}{rrr}{cos} \left( a \right)&0&{sin} \left( a \right)\\0&1&0\\-{sin} \left( a \right)&0&{cos} \left( a \right)\\\end{array}\right) \cdot \vec{v} \)\(= \left( \begin{array}{r}-\operatorname{cos} \left( a \right) - 4 \; \operatorname{sin} \left( a \right) \\ -8 \\ -4 \; \operatorname{cos} \left( a \right) + \operatorname{sin} \left( a \right) \end{array} \right)\)

Ebene x=0

Drehung um

\( \left(\begin{array}{rrr}\frac{4}{17} \; \sqrt{17}&0&\frac{-1}{17} \; \sqrt{17}\\0&1&0\\\frac{1}{17} \; \sqrt{17}&0&\frac{4}{17} \; \sqrt{17}\\\end{array}\right)\)