Hallo Werner-Salomon, vielen Dank für deine Antwort: Genauer geht es mir um den weißen Punkt, den möchte ich so rotieren, wie die blaue Box, nicht die rote Box. Ich habe wohl irgendwo einen Denkfehler.
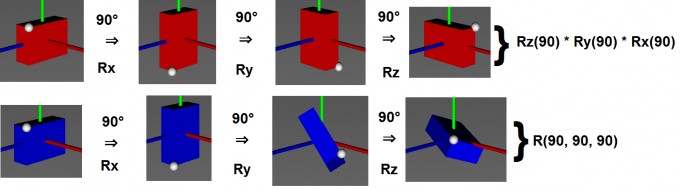 Die rote Box wird erst um 90° um den Rx(90) rotiert, dann Ry(90), dann Rz(90). Der Punkt P befindet sich auf Koordinate P (0.5, 1.0, 1.5). Wenn ich ausrechne: Rz(90) * Ry(90) * Rx(90) * P, dann erhalte ich als Ergebnis den Punkt P_res = (1.5, 1.0, -0.5). Das ist der Punkt von der roten Box, nicht von der blauen.
Die rote Box wird erst um 90° um den Rx(90) rotiert, dann Ry(90), dann Rz(90). Der Punkt P befindet sich auf Koordinate P (0.5, 1.0, 1.5). Wenn ich ausrechne: Rz(90) * Ry(90) * Rx(90) * P, dann erhalte ich als Ergebnis den Punkt P_res = (1.5, 1.0, -0.5). Das ist der Punkt von der roten Box, nicht von der blauen.
Jetzt würde ich gerne wissen, wie ich die Transformationsmatrizen so multiplizieren kann, dass ich den Punkt um alle Achsen gleichzeitig rotieren kann. Das Ergebnis müsste so aussehen: R(90, 90, 90) = ~ (1.30 0.42 1.30).
Grund: In VRML gibt es dich Möglichkeit eine rotation durch Angabe von drei Punkten und einem Winkel durchzuführen. Dazu finde ich aber keine Rotationsmatrix, das das macht. Die obigen Rotationsmatrizen führen die Berechnung der roten Box durch, nicht der blauen.
Ich suche also die Transformationsmatrix für die Rotation um alle 3 Achsen gleichzeitig, nicht nacheinander.
Vielen Dank schonmal für dein Interesse/Mühe.