Winkelberechnung nach Rotation um Achsen

Question

ich bin seit einigen Tagen vor einem Problem. 

Folgende Situation:

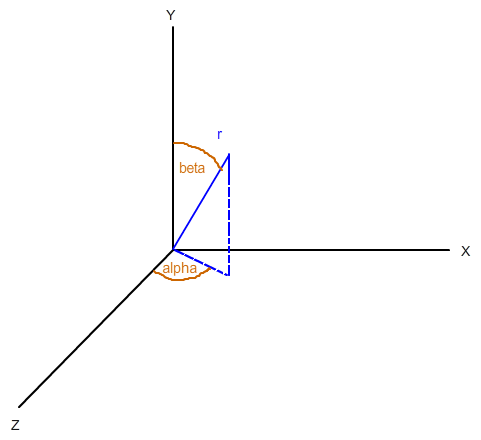
Ich habe einen Vektor im 3D Raum beschrieben mit der Länge( r) und 2 winkel( alpha, beta (siehe skizze)), wobei alpha den Winkel von der projektion des Vektors auf der XZ-Ebene bestimmt und beta denk winkel zur Y-Achse. Meines Wissens nach sollte dies ausreichend sein um jeden Punkt im Raum beschreiben zu können. nun Will ich den Vektor beispielsweise um die x,y und z achse um 10° rotieren. Wenn ich um Y rotieren möchte, muss ich ja lediglich alpha um 10° in die gewünschte richtung ändern.

 

Jetzt zum eigentlichen Problem:

Ich möchte den Vektor, bzw. der Punkt der daraus resultiert auch um die X und Z Achse rotieren (z.B. um 10°), hab jedoch keine Ahnung wie, oder was für eine Formel ich benötige, da eine rotation um X als auch um Z ja jeweils Einfluss auf beide Winkel haben muss.

 

Meine Internet-Recherchen waren leider allesamt erfolglos, da ich mein Problem nicht richtig beim Namen nennen kann, ich hoffe ihr könnt mir da weiterhelfen. Zum besseren Verständnis noch eine kleine Skizze.

 

:)

 

Comments

Momentan würde ich als Lösung vorschlagen die Koordinaten auszurechnen. Braucht ja nur die Winkelumrechnung auf dem Einheitskreis sein.

Auf die Koordinaten die Drehmatrix anwenden und dann die Koordinaten wieder in Winkel zurückwandeln.

Answer 1

Die Rotationsmatrix war auch eine meiner Überlegungen, aber auf mein Problem nicht wirklich anwendbar, da ich keine Punkte hab, auch die länge "r" ist rein fiktiv.

Gibt es denn keine Möglichkeit die 2 winkel nach einer beliebigen rotation neu zu bestimmen, ohne Absolute Punkte zur Hilfe nehmen zu müssen?

Comments

Wie ich bereits geschrieben habe kommt es auf r ja auch nicht drauf an. Du rechnest nur die Winkel in Koordinaten auf der Einheitskugel aus. Damit liegen alle Koordinaten zwischen -1 und +1. Diese Einheitskoordinaten drehst du dann und wandelst sie dann wieder zurück in die Winkel. Das r bleibt fiktiv einfach bestehen.

Eventuell kannst du das ganze auch allgemein machen und sehen, falls sich da etwas vereinfachen lässt.

---

sry, Einheitskugel war wohl das richtige Stichwort, leider steh ich nun vor dem nächsten Hindernis :(

Ich habe weder mit Kugelkoordinaten  Erfahrung noch, mit dem "kartesisches Koordinatensystem" ,was ich dazu gefunden hab, schon mal was gerechnet.  Könntest du mir vielleicht ein Beispiels (zb.alpha=60, beta=30, rotation um x-achse um 10°) vorrechnen :/

Answer 2

Die Einheitskugelkoordinaten würden dann lauten:

x = sin(beta) * sin(alpha)
y = cos(beta)
z = sin(beta) * cos(alpha)

Das kannst du jetzt durch die Drehmatrix schicken.

Beim Rückwandeln gilt

alpha = tan^{-1}(x / z)
beta = tan^{-1}(y / √(x^2 + z^2))

Ich habe das jetzt nicht geprüft also bitte vorher mal prüfen.

Comments

Vielen dank. Werde ich heute testen :)

---

Hi leute,

ich habe das gleiche Problem. Ich befasse mich gerade auch mit R^3 Rotationen. Ich benutze die RotationsMatrizen zum ermitteln der Koordinaten. Bei einer Verdrehung um nur einer Achse ist alles ok. Sobald eine zweite, geschweige denn noch eine dritte hinzu kommt, passt gar nichts mehr.

Ich habe nun herausgfunden dass sich die Winkel bei zwei oder dreih Drehungen ändern. Verstehen kann ich das momentan aber nicht. Und berechnen schon gar nicht.

Z.B. Ich einen Punkt im R^3 um Rz=1, Ry=4 und Rx=80 Grad drehen. Nun habe ich ein kleines Tool wo dies berechnet. Ist ja alles schön und gut. Aber ich will verstehen warum es folgende Rotationen anzeigt: Rz=3,766, Ry=-1,679 und Rx= -80,02 Grad.

Vieleicht kann mir jemand eine kleine "Erleuchtung" geben dass ich nicht so im dunkeln tappe.

MfG

---

Stell bitte deine Frage neu ein und zwar mit allem was dir vorliegt.

---

Kommentar von hugoboss ist doppelt zu https://www.mathelounge.de/456483/transformationsmatrix-rotation-drei-achsen-gleichzeitig.