Hallo,
Herr Hausmann hat gehört, dass ein Quadrat das Rechteck ist, das für einen festen Umfang den größten Flächeninhalt besitzt.
Trifft das auch für ein offenes Rechteck zu?
Die Antwort ist JA! es trifft immer zu - man muss aber das Quadrat zunächst mal wiederfinden! Betrachten wir dazu zunächst ein beliebiges Rechteck und fragen uns, wie es bei konstantem Umfang(!) aussehen muss, damit sein Flächeninhalt maximal wird:
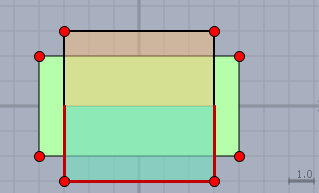
Antwort: wie ein Quadrat. Das abgebildete Rechteck und das Quadrat haben beide den gleichen Umfang von 24. Das Quadrat ist mit einem Flächeninhalt von 36 aber um 4 größer als das Rechteck mit einer Fläche von 32.
Wichtig: was für das ganze Rechteck bzw. Quadrat gilt, gilt auch für halbe Rechteck bzw. das halbe Quadrat. Auch das halbe Quadrat ist größer als das halbe Rechteck. Und beide Hälften haben den gleichen 'Umfang' von 12 - exklusiv der Strecke, wo beide Flächen halbiert worden sind.
Folglich schein die rot markierte Form einer rechteckigen Dachrinne, die genau ein halbes Quadrat darstellt, die in der Fläche maximale zu sein.
Wenn ich die Höhe dieses halben Quadrats mit \(a\) bezeichne, so ist die Breite \(2a\). Variiere ich die Höhe um ein Maß \(x\) - das kann positiv oder negativ sein - so wird die Höhe zu \(a+x\) und die Breite zu \(2(a-x)\). Die Fläche \(F\) inklusive dieser Variation wäre dann$$F = (a+x) \cdot 2(a-x) = 2(a^2 - x^2)$$D,h, unabhängig vom Vorzeichen von \(x\) wird die Fläche \(F\) immer kleiner, wenn \(x\) von \(0\) abweicht.
Daraus folgt: die Bauform einer rechteckigen nach oben offenen Dachrinne hat bei konstantem Materialeinsatz, genau dann das maximales Fassungsvermögen, wenn Breite zu Höhe sich wie \(2\div 1\) verhalten.
In Deinem konkreten Fall wären das eine Breite von \(25\, \text{cm} / 2 = 12,5\,\text{cm}\) und eine Höhe von \(25\,\text{cm}/4 = 6,25\, \text{cm}\).
Gruß Werner