Querschnitt eines Kanals, maximale Wasseroberfläche bestimmen

Question

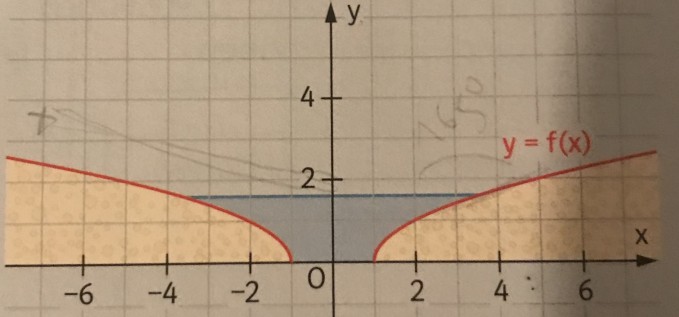
Aufgabe:

Die Skizze (nicht maßstäblich) zeigt den Querschnitt eines Hochwasserüberlaufkanals. Die y-Achse ist Symmetrieachse des Querschnitts. Eine der beiden Böschungslinien kann näherungsweise in einem kartesischen Koordinatensystem durch die Funktion f mit f f(x)=√(x−1) (x ∈ Df) beschrieben werden. Eine Längeneinheit entspricht einem Meter. Der maximale Pegel beträgt 2,0 m, der Normalpegel 1,6 m.
a) Geben Sie die Breite der Wasseroberfläche bei maximalem Pegel an.
c) Ein kritischer Pegel wird erreicht, wenn der Neigungswinkel der Böschungslinie gegenüber der Wasseroberfläche 165° überschreitet.
Ermitteln Sie einen Näherungswert für diesen kritischen Pegel.
d) Von einem Punkt P(10 | 5) aus soll der Kanal überwacht werden. Untersuchen Sie, ob bei Normalpegel die gesamte Breite der Wasseroberfläche einsehbar ist.

Problem/Ansatz:

Ich weiß, dass bei a 10 herauskommt, aber ich verstehe nicht wie. Und ohne a kann ich die restlichen Aufgaben auch nicht bearbeiten 

Answer 1

√(x - 1) = 2   | ()^2

x - 1 = 2^2   | + 1

x = 2^2 + 1 = 5

Wir haben also 5 m rechts und 5 m links von der y-Achse. Ist das so klar? Du kannst den Wert ja auch etwa ablesen, wenn du dir die Gerade mit y = 2 mal einzeichnest.

~plot~ sqrt(x-1);sqrt(-x-1);2 ~plot~

Answer 2

Berechne den Schnittpunkt der Geraden y=2 (Darstellung des Maximalpegels) mit dem Graphen von f.