Der Kanal soll an seiner steilsten Stelle die Steigung 10 % haben. Bestimmen Sie k. Querschnitt eines Kanals.

Question

Aufgabe:

Der Querschnitt eines Kanals soll durch eine Funktion \( f_{k} \) mit \( f_{k}(x)=1-e^{-k x^{2}} \) beschrieben werden (eine Längeneinheit entspricht \( 10 \mathrm{~m} \) ). In Fig. 1 ist der Querschnitt für \( k=1 \) abgebildet.

a) Der Kanal soll an seiner steilsten Stelle die Steigung \( 10 \% \) haben. Bestimmen Sie \( k \).

b) Eine Person mit Augenhöhe 1,7 m geht auf der Geraden \( y=1 \) von links auf den Kanal zu. Berechnen Sie in Abhängigkeit von \( k \) den Punkt auf dieser Geraden, an dem diese Person alle Punkte des leeren Kanals einsehen kann.

Answer 1

f(x) = 1 - e^{- k·x^2}

f'(x) = 2·k·x·e^{- k·x^2}

f''(x) = 2·k·e^{- k·x^2}·(1 - 2·k·x^2) = 0 --> x = ± √(1/(2·k))

f'(√(1/(2·k))) = √(2·k/e) = 0.1 --> k = e/200 = 0.01359

Comments

Ich habe die Wendestelle nun in die 1. Ableitung eingesetzt => 

f'(√(1/(2·k))

Wie komme ich jetzt zum nächsten Schritt, also

√(2·k/e)

Wie ist dort der Rechenweg?

Ich würde mich über eine Antwort freuen. :)

---

Probier es doch mal selber und frag nach, wenn du es nicht selber schaffst und sag dann auch bitte, wo du nicht weiter weist.

Alternativ gäbe es die Möglichkeit sich von einer elektronischen Rechenhilfe unterstützen zu lassen.

---

\( \begin{aligned} f^{\prime}\left(\sqrt{\frac{1}{2 k}}\right) &=2 \cdot k \cdot \sqrt{\frac{1}{2 k}} \cdot e^{\left.-k \cdot \sqrt{\frac{1}{2 k}}\right)^{2}} \\ &=2 k \cdot\left(\frac{1}{2 k}\right)^{\frac{1}{2}} \cdot e^{-k \cdot \frac{1}{2 k}} \\ &=2 k \cdot(2 k)^{-\frac{1}{2}} \cdot e^{-\frac{1}{2}} \\ &=2 k^{\frac{1}{2}} \cdot e^{-\frac{1}{2}} \\ &=\frac{2 k^{\frac{1}{2}}}{e^{\frac{1}{2}}}=\left(\frac{2 k}{e}\right)^{\frac{1}{2}} \\ &=\sqrt{\frac{2 k}{e}} \end{aligned} \)

---

a) habe ich gelöst bekommen mit k ≤ e/200.
Kann mir bitte jemand bei b) erklären, was hier eigentlich gemeint ist wenn er von links kommt? Schwebt er da über dem Kanal oder läuft er den Abhang herunter? Uns was ist mit alle Punkte des Kanals gemeint, die er sehen soll? Nur die unterhalb vor ihm? Ich denke die Grundidee wird sein, daß die Blickgerade den Hang nicht schneiden darf und ich sozusagen über den Wendepunkt deüber schauen kann. Darf ich die Bedingung an k aus a) verwenden?

---

Mein Aufgabentext bei a) weicht übrigens ein bisschen ab:

Der Kanal soll eine Steigung von maximal 10% haben. Bestimmen Sie die Werte von k.

---

Schwebt er da über dem Kanal oder läuft er den Abhang herunter?

Er läuft hinunter. Von links her kommend.

Nur die unterhalb vor ihm?

Nicht nur die auf der anderen, rechten Kanalseite, sondern auch die unterhalb von ihm.

Ich denke die Grundidee wird sein, daß die Blickgerade den Hang nicht schneiden darf

Ja.

---

Er läuft hinunter. Von links her kommend.

Bist Du sicher? Wenn er auf der Geraden y=1 kommt, befand er sich ja nie auf dem Graphen der Kurve. Von hinunterspringen ist nicht die Rede… Und was soll dann überhaupt die Angabe y=1?

---

Bei y = 1 sind vor dem Hinuntergehen (nicht -springen) die Füße. Die Augen entsprechend höher.

---

Für die Querschnittsfunktion ist kein Definitionsbereich angegeben. Es ist in der Aufgabe festgelegt, dass die Person auf y=1 "schwebt". Dein Ansatz mit der Blickgeraden ist richtig

---

@Döschwo: Die Füsse (und der Rest) waren also in der Luft, da f(x) immer kleiner als 1 ist. Also müßte er diese Differenz einmal ‚runterspringen‘.

@Mathhilf: So sehe ich das auch

---

Ich denke die Grundidee wird sein, daß die Blickgerade den Hang nicht schneiden darf und ich sozusagen über den Wendepunkt deüber schauen kann. Darf ich die Bedingung an k aus a) verwenden?

Die Grundidee ist richtig. Du kannst im linken Wendepunkt der Funktion die Wendetangente aufstellen und dich fragen, bei welchem x sie eine Höhe von 1 + 0.17 = 1.17 hat. Da du alles in Abhängigkeit von k berechnen sollst, ist es normal, dass dein k noch im Term mit bleiben soll.

Als Punkt hätte ich z.B. (- √2·(17·e^(1/2) + 200)/(200·√k) | 1) ≈ (- 1.612/√k | 1) heraus.

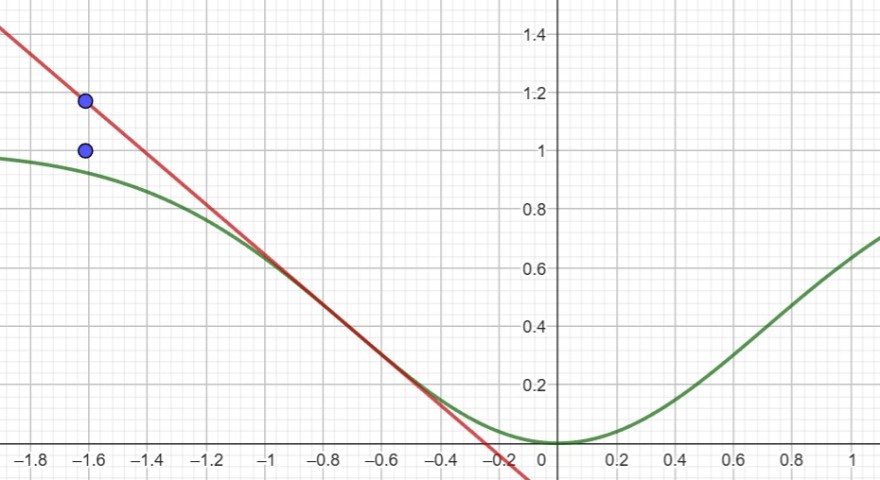
Ich skizziere mit k = 1 also mal den Kanal, die Tangente und den Punkt auf der Geraden y = 1 und den Augenpunkt auf der Tangente.

---

eine Längeneinheit entspricht 10m

---

Danke, so hatte ich das auch überlegt, bin aber auf was ganz krummes als x Koordinate des Punktes gekommen:

x₀ = - \( \sqrt{\frac{2}{k}} \) - 0.17 \( \sqrt{\frac{e}{2k}} \)

---

@user26605

Danke für den Hinweis. Ich habe es korrigiert.

---

Wenn er weit genug weg ist, kann einen Teil nicht sehen:

---

Danke, so hatte ich das auch überlegt, bin aber auf was ganz krummes als x Koordinate des Punktes gekommen:

Das sieht so doch sehr gut aus. Ich hatte zuerst nur die LE von 10 m nicht beachtet. Komme aber in der Berichtigung auch auf deine Stelle. Mein Programm notiert das nur anders.