Hallo,
mache Dir zunächst eine Skizze, die das Szenario als Projektion auf die XY-Ebene darstellt. Die Grundfläche der Pyramide liegt in der XY-Ebene.

Die Geradengleichung in x,y kannst Du berechnen aus$$g_{xy}: \quad \begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}56\\ -44\end{pmatrix} + \begin{pmatrix}-8\\ 8\end{pmatrix} t \\ \begin{aligned} \implies x &= 56 - 8t \\ t &= -\frac 18 x + 7 \\ \implies y &= -44 + 8\left( -\frac 18 x + 7\right) = -x + 12 \end{aligned}$$wie man sieht, durchquert die Gerade die Grundfläche. Die Höhe der Gerade bei \(F_1\) ist \(z=15\). Von dort senkt sich die Gerade Richtung Pyramide ab.
Der kritische Punkt liegt also bei der Kante \(CS\) der Pyramide. Wenn die Gerade dort noch oberhalb der Kante liegt, gibt es keinen Schnittpunkt. Da die Kante \(CS\) in der YZ-Ebene liegt, berechnet man den Schnittpunkt von \(g\) mit der YZ-Ebene.$$\begin{aligned} x=0 &= 56 + (-8)r_{yz} \implies r_{yz} = 7 \\ g(r=7) &= \begin{pmatrix}0\\ 12\\ 8\end{pmatrix}\end{aligned} $$Die Höhe der Geraden über der XY-Ebene ist dort 8 und die Kante \(CS\) hat aber nur die Höhe 3, wie sich leicht prüfen lässt.
Also liegt KEIN Schnittpunkt der Geraden mit der Pyramide vor!
Folgendes Bild zeigt das nochmal:
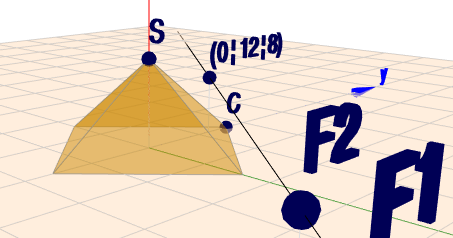
(klick auf das Bild, dann kannst Du die Szene mit der Maus rotieren und bekommst einen besseren räumlichen Eindruck)