Aufgabe:
Umformen zeigen, ob die Funktionen u1 und u2 fur ¨ x > 0 gleich sind
Problem/Ansatz:
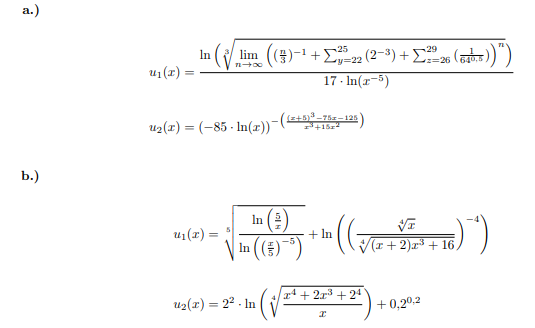
Text erkannt:
a.)
$$ \begin{array}{l} u_{1}(x)=\frac{\ln \left(\sqrt[3]{\lim \limits_{n \rightarrow \infty}\left(\left(\frac{n}{3}\right)^{-1}+\sum \limits_{y=22}^{25}\left(2^{-3}\right)+\sum \limits_{z=26}^{29}\left(\frac{1}{64^{0,5}}\right)\right)^{n}}\right)}{17 \cdot \ln \left(x^{-5}\right)} \\ u_{2}(x)=(-85 \cdot \ln (x))^{-\left(\frac{(x+5)^{3}-75 x-125}{x^{3}+15 x^{2}}\right)} \end{array} $$
b.)
$$ u_{1}(x)=\sqrt[5]{\frac{\ln \left(\frac{5}{x}\right)}{\ln \left(\left(\frac{x}{5}\right)^{-5}\right)}}+\ln \left(\left(\frac{\sqrt[4]{x}}{\sqrt[4]{(x+2) x^{3}+16}}\right)^{-4}\right) $$
$$ u_{2}(x)=2^{2} \cdot \ln \left(\sqrt[4]{\frac{x^{4}+2 x^{3}+2^{4}}{x}}\right)+0,2^{0,2} $$
Ich soll durch Umformen zeigen, ob die Funktionen u1 und u2 fur ¨ x > 0 gleich sind.