Wie muss man hier vorgehen RxR?

Question

Aufgabe:

Text erkannt:

Sei \( A=\{(x, y) \in \mathbb{R} \times \mathbb{R} \mid 2 x-y+3=0\} \) und \( B=\left\{(x, y) \in \mathbb{R} \times \mathbb{R} \mid x^{2}-y=0\right\} \)
Geben Sie die Menge \( A \cap B \) an.

Text erkannt:

Sei \( A=\{(x, y) \in \mathbb{R} \times \mathbb{R} \mid 2 x-y+3=0\} \) und \( B=\left\{(x, y) \in \mathbb{R} \times \mathbb{R} \mid x^{2}-y=0\right\} \)
Geben Sie die Menge \( A \cap B \) an.

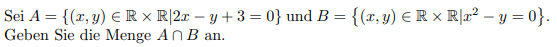
Problem/Ansatz

Wie muss man hier vorgehen? Was bedeutet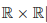

Text erkannt:

\( \mathbb{R} \times \mathbb{R} \)

Was wäre die Lösung dazu und wie kommt man darauf?

Answer 1

Aloha :)

Ein Punkt \((x;y)\in\mathbb R\times\mathbb R\) hat eine Koordinate \(x\in\mathbb R\) und eine Koordinate \(y\in\mathbb R\). Wenn dieser Punkt in der Schnittmenge beider Mengen liegen soll, muss er beide Bedingungen erfüllen:$$2x-y+3=0\quad\text{und}\quad x^2-y=0$$Aus der zweiten Gleichung entnehmen wir \(y=x^2\) und setzen das in die erste Gleichung ein:$$2x-x^2+3=0\implies x^2-2x-3=0\implies(x-3)(x+1)=0$$Wegen des Satzes vom Nullprodukt haben wir zwei Punkte$$x=-1\implies y=(-1)^2=1$$$$x=3\implies y=3^2=9$$und können die Schnittmenge angeben:$$A\cap B=\{(-1;1)\,,\,(3;9)\}$$