Aufgabe:
Hallo. Ich habe hier eine Aufgabe zur Grenzwertberechnung. Die Lösung habe ich von meinem Dozenten, jedoch verstehe ich bei einem Schritt nicht die Umformung. Wie kommt man vom rechten oberen Ausdruck auf den darunter, rechts unten in lila farben? Kann mir das jemand bitte erklären. Danke für Eure Mühe. LG
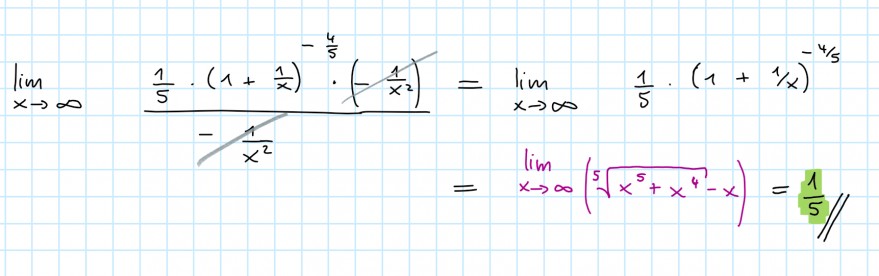
Text erkannt:
\( \lim \limits_{x \rightarrow \infty} \frac{\frac{1}{5} \cdot\left(1+\frac{1}{x}\right)^{-\frac{4}{5}} \cdot\left(-\frac{1}{x^{2}}\right)}{\frac{-1}{x^{2}}}=\lim \limits_{x \rightarrow \infty} \frac{1}{x \rightarrow \infty}\left(\sqrt[5]{x^{5}+x^{4}}-x\right)=\frac{1}{5} / / \)