Folgende Aufgabenstellung(en):
Aufgaben:
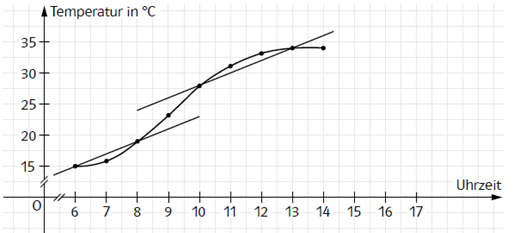
1) Es sind 2 Sekanten eingezeichnet, die parallel verlaufen. Was bedeutet das in diesem Kontext?
Die mittlere Temperaturänderungen von 6h bis 14h (?)
2) Lies aus dem Graphen ab zwischen welchen beiden Stunden die Temperaturänderung
am größten ist. Wie groß ist diese ungefähr?
Von 6 bis 8 Uhr: 4°C (?)
Von 10 bis 13 Uhr: 6,5°C (?)
3) Berechne die mittlere Temperaturänderung von 6h bis 14h
(Nimm um 6h eine Temperatur von 15°C an und um 14h eine Temperatur von 34°C)
[6h; 14h]
a = ? b = ?
4 ) Berechne weiters die mittleren Temperaturänderungen in den Intervallen [7h;10h], [8h;13h],
und [10h;14h].
Lies dazu die zugehörigen Temperaturen möglichst genau ab (ganz genau geht es natürlich nicht).
1) und 2) habe ich versucht, zu beantworten. Bin mir aber nicht ganz sicher, was die Richtigkeit angeht..
bei 3) und 4) bin ich grad im Unklaren: Wie schreibe ich das Intervall an? Habe zwar [6h; 14h] geschrieben, aber könnte es auch nicht sein, dass die Temperatur in der Klammer steht? Und wie berechne ich a und b, um schließlich die mittlere Temperaturänderung mit der Formel (f(b) - f(a)/b-a) zu berechnen? Oder ist die Temperatur um 6h bzw. um 14h stellvertretend für a und b?
Wäre über eure Hilfe sehr dankbar!!