Also wie kann denn die eine gerade überhalb oder unterhalb der anderen liegen?

Question

Aufgabe:

Hallo, ich hätte eine Frage bezüglich Linearen Ungleichheiten und wie man sie darstellt:

Also wenn man nun die beiden geraden f(x)=x-3 und g(x)=-2x+0 hat (Der Schnittpunkt liegt bei (-1/-2), warum schreibt man

x<1 : g>f

x>1 : f>g.

Also wie kann denn die eine gerade überhalb oder unterhalb der anderen liegen?

Problem/Ansatz:

Es wäre sehr nett wenn mir jemand helfen könnte.

Answer 1

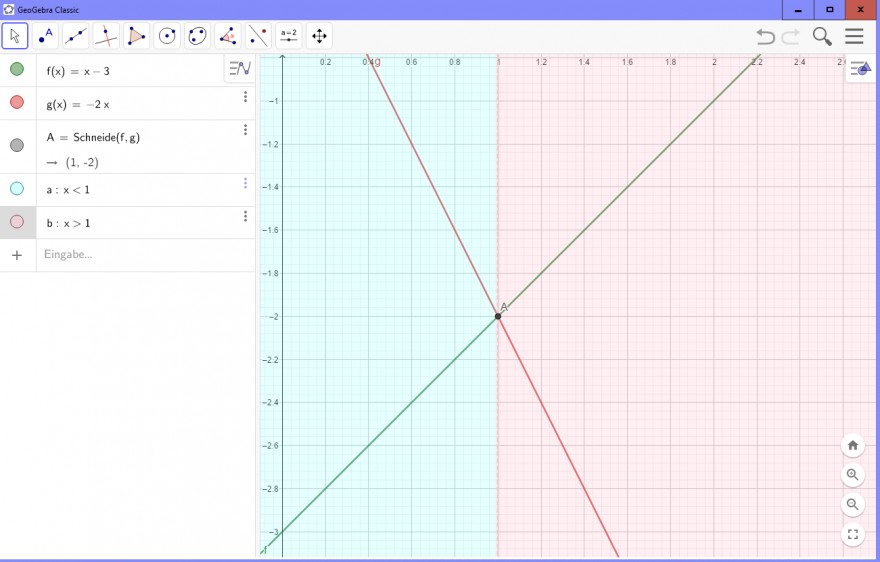
Bei zwei Geraden, bei denen die Steigung positiv und negativ ist, ist die Gerade oberhalb, die die negative Steigung hat.

Text erkannt:

\( f(x)=x-3 \)
\( g(x)=-2 x \)
O \( A= \) Schneide \( (f, 8) \)
$$ -(1,-2) $$
\( a=x<1 \)
\( b: x>1 \)
Eingabe.

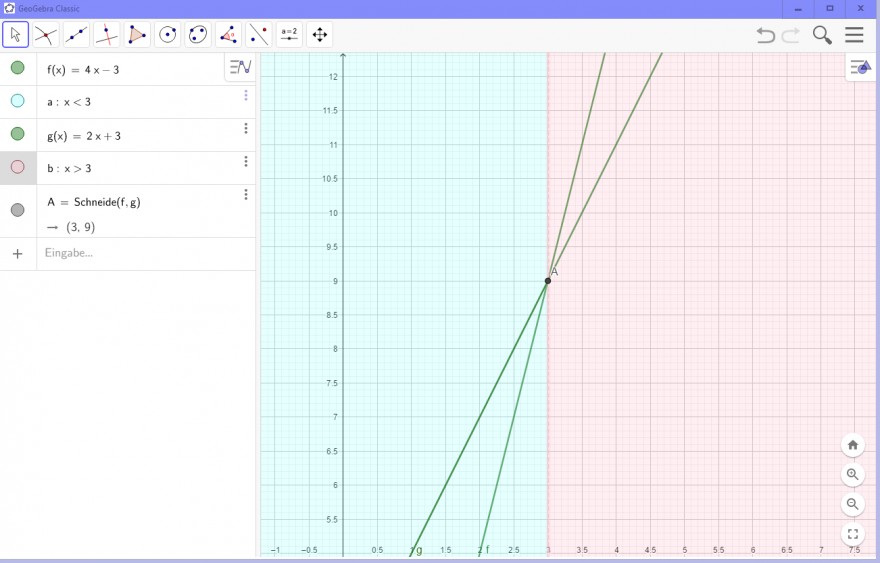
Bei zwei Geraden, bei denen die Steigung zweimal positiv ist, ist die Gerade oberhalb, die die größere Steigung hat.

Text erkannt:

\begin{tabular}{l}
\( \quad f(x)=4 x-3 \) \\
\hline
\end{tabular}
\( =N \)
\begin{tabular}{l}
\( a: x<3 \) \\
\hline
\end{tabular}
\( g(x)=2 x+3 \)
\( b>3 \)
0
\( A= \) Schneide \( (f, 8) \)
$$ -(3.9) $$
+ Eingabe-

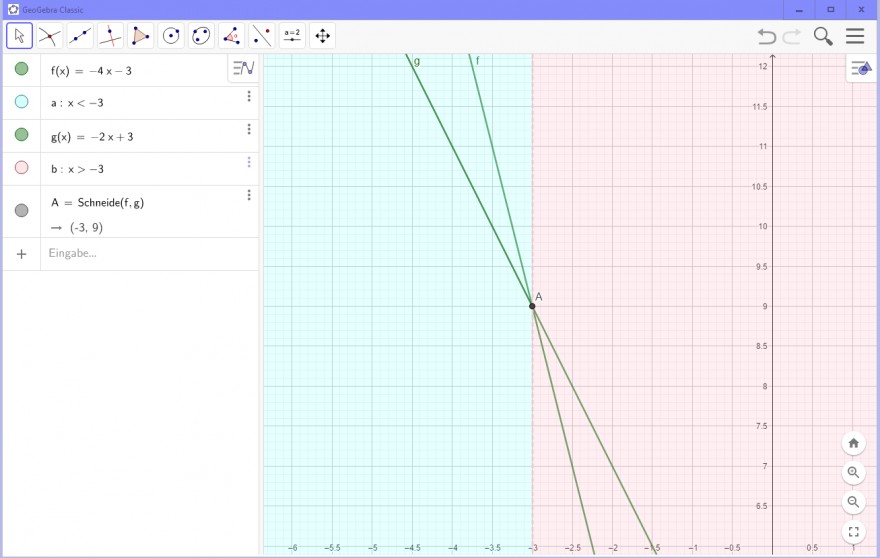
Bei zwei Geraden, bei denen die Steigung zweimal negativ ist, ist die Gerade oberhalb, die die kleinere Steigung hat.

Text erkannt:

A \( x \) :
\( f(x)=-4 x-3 \)
IN
a : \( x<-3 \).
\( g(x)=-2 x+3 \)
\( b: x>-3 \)
\( \mathrm{A}= \) Schneide \( (\mathrm{f}, \mathrm{g}) \)
\( \rightarrow(-3,9) \)
+ Eingabe-.

Answer 2

Also wenn man nun die beiden geraden f(x)=x-3 und g(x)=-2x+0 hat (Der Schnittpunkt liegt bei (-1/-2), warum schreibt man

Der Schnittpunkt liegt bei (1 | -2)

Und für x > 1 verläuft f über dem graphen von g.
f(x) > g(x) für x > 1

Und für x < 1 verläuft f unter dem graphen von g.
f(x) < g(x) für x < 1

Skizze

~plot~ x-3;-2x ~plot~

Comments

Ok, und wie würde es für f(x)=-2x+8 und g(x) = -4x+12 aussehen?

x > 2 : f > g
x < 2 : g > f

~plot~ 8-2x;12-4x;[[-12|12|-8|8]] ~plot~

Answer 3

Ich habe mal eine Zeichnung angefertigt, die dir zeigt, wie aus x<1  eben g > f folgt

und somit auch aus  x > 1  → f > g folgt.

mfG

Moliets

Text erkannt:

0
\( f(x)=x-3 \)
\( g(x)=-2 x \)
\( \mathrm{A}= \) Schneide \( (\mathrm{f}, \mathrm{g}, 1) \)
\( \rightarrow(1,-2) \)
\( a: x<1 \)
\( \mathrm{b}: x>1 \)
Eingabe..

Comments

Ok, und wie würde es für f(x)=-2x+8 und g(x) = -4x+12 aussehen?

---

Da, wo sie sich schneiden, wechseln die beiden Geraden das "oben" und "unten".

---

Wie definiert man denn „oben“?

---

Wie definiert man denn „oben“?

Größere y-Koordinaten für gleiche x-Koordinaten.

---

Ah ok. Vielen Dank! Ihr habt mir sehr weitergeholfen .

---

Der Punkt B liegt oberhalb von Punkt D . Der y -Wert von B ist größer als der y-Wert von D.

Der Punkt A liegt unterhalb von Punkt C . Der y -Wert von A ist kleiner als der y-Wert von C .

mfG

Moliets