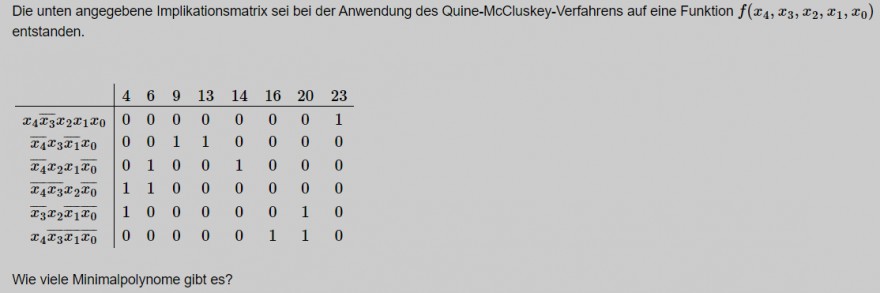
Text erkannt:
Die unten angegebene Implikationsmatrix sei bei der Anwendung des Quine-McCluskey-Verfahrens auf eine Funktion \( f\left(x_{4}, x_{3}, x_{2}, x_{1}, x_{0}\right) \) entstanden.
\begin{tabular}{c|cccccccc}
& 4 & 6 & 9 & 13 & 14 & 16 & 20 & 23 \\
\hline\( x_{4} \overline{x_{3}} x_{2} x_{1} x_{0} \) & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
\( \overline{x_{4}} x_{3} \overline{x_{1}} x_{0} \) & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\
\( \overline{x_{4}} x_{2} x_{1} \overline{x_{0}} \) & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\
\( \overline{x_{4} x_{3}} x_{2} \overline{x_{0}} \) & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
\( \overline{x_{3}} x_{2} \overline{x_{1} x_{0}} \) & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
\( x_{4} \overline{x_{3} x_{1} x_{0}} \) & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0
\end{tabular}
Wie viele Minimalpolynome gibt es?
Aufgabe: