Problem: Negativer Steigungswinkel
Liebe Lounge,
ich habe eine Frage zum Thema Steigung/Neigungswinkel von Funktionen.
Das Konzept ist mir bekannt und klar.
Ich suche nach einer detaillierten Erklärung, weshalb der Steigungswinkel negativ ist (ist er das legitimerweise überhaupt, oder MUSS in einem solchen Fall noch mit 180° addiert werden?).
Es hat sicherlich mit dem arkustangens zu tun, welcher ja für Argumente kleiner 0 negative Werte ausspuckt.
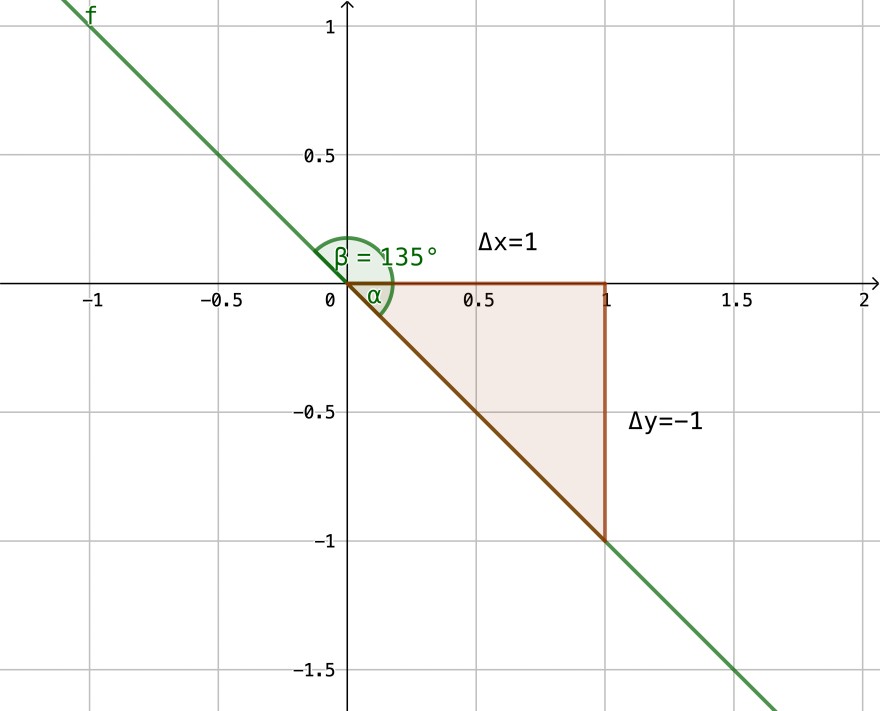
Ich versuche es mal zu erklären und bin auf Rückmeldung gespannt: Angenommen man definiert den Steigungswinkel als den im positiven Drehsinn gemessenen Winkel zwischen x-Achse und Gerade. Dann kommt man an dieser Stelle mit tan(alpha)=m nicht zum gewünschten Winkel.
Deshalb gehe ich mal anders vor: Wir berechnen zunächst den Winkel alpha des Dreiecks (in diesem Fall betrachten wir nur positive Seitenlängen). Also: tan(alpha)=1 <--> alpha=45°
Um jetzt auf den Steigungswinkel ß zu kommen gilt: ß = 180° - 45° = 180° + (-45)° = (-45°)+180°=arkustan(-1)+180° =arkustan(m)+180°...
Besser kann ich es nicht herleiten ... Gibt es jemand, der es besser kann?
LG und
Kombi