Berechne den Abstand zwischen S und A.

Question

Aufgabe:

Es seien A und B zwei Punkte auf einer Geraden im Abstand von 10 LE. Eine weitere Gerade g schneidet diese im Winkel von 45° im Punkt S. Sei C ein weiterer Punkt auf g mit AC+BC=30. Weiter sei der Winkel zwischen AC und g gleich dem Winkel zwischen BC und g.

Berechne den Abstand zwischen S und A.

Problem/Ansatz:

Meine Idee war der Sinussatz, damit komme ich auf AS=10/AB-BC. Das hilft mir aber nicht weiter, weil ich ja nicht AB-BC sondern AC+BC kenne. Hat jemand eine Idee wie ich das lösen kann oder einen anderen Ansatz? Vielen Dank!!!

Answer 1

Hallo Peter,

hast Du Dir schon mal eine Zeichnung gemacht? Ich komme zu folgendem Szenario:

 

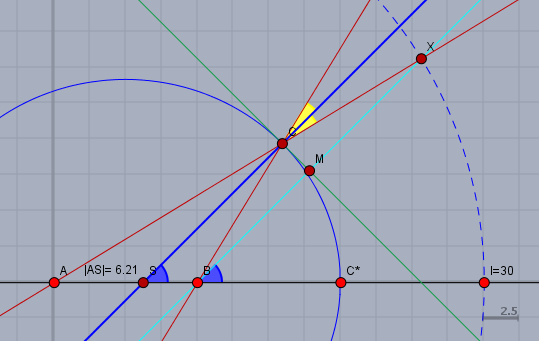
Wobei ich annehme, dass sich der Winkel von 45° in Richtung \(B\) öffnet. Man kann die Punkte \(A\) und \(B\) auch vertauschen, was dann zu einer zweiten Lösung führt. Alle Punkte \(C\), deren Abstandssumme zu \(A\) und \(B\) gleich \(30\) ist, liegen auf einer Ellipse, mit den Brennpunkten \(A\) und \(B\), die durch einen Punkt \(C^*\) verläuft, der das Spiegelbild von \(A\) an \(B\) ist.

Wenn der Winkel zwischen AC und g gleich dem Winkel zwischen BC und g sein, soll, dann muss \(g\) (blau) mit der Winkelhalbierenden der Geraden durch \(AC\) und \(AB\) (beide rot)  zusammen fallen. Die gleichen Winkel habe ich gelb eingezeichnet. Die 45° sind blau gezeichnet.

Die Tangente \(t\) (grün) an der Ellipse im Punkt \(C\) steht senkrecht auf der Winkelhalbierenden und damit senkrecht auf \(g\). Denkt man sich die Ellipse in einem Koordinatensystem mit Ursprung in \(A\) und \(B\) bei \(B(10|\, 0)\), dann ist die Steigung der Tangente \(-1\). So lässt sich der Punkt \(C\) finden. Die Senkrechte zu \(t\) in \(C\) schneidet die X-Achse dann in \(S\).

Falls Du noch Fragen dazu hast, so melde Dich bitte.

Comments

Tut mir leid, aber ich habe noch nicht verstanden, wie man C jetzt findet. Wie kann man mit der Bedingung, dass diese Tangente die Steigung -1 hat C finden? Vielen Dank schon mal, die Skizze hilft auf jeden Fall, meine sah bisher etwas unübersichtlich aus ;-)

---

Tut mir leid, aber ich habe noch nicht verstanden, wie man C jetzt findet.

Stelle die Gleichung für die Ellipse auf. Die Halbachsen sind \(a=15\) und \(b=\sqrt{200}\) (Warum?). In der ersten Hauptlage hätte die Ellipse die Gleichung$$\frac{x^2}{15^2} + \frac{y^2}{200} = 1$$Wenn Du es so machst, wie ich es gezeichnet habe, muss die Ellipse noch um \(10/2=5\) nach rechts verschoben werden. Das macht$$\frac{(x-5)^2}{15^2} + \frac{y^2}{200} = 1$$Das kann man direkt ableiten und \(y'=-1\) setzen:$$\begin{aligned} \frac{2(x-5)}{15^2} + \frac{2yy'}{200} &= 0 &&|\, y'=-1 \\ 8(x-5) + 9y\cdot (-1) &= 0 \\ y &= \frac 89(x-5)\end{aligned}$$Einsetzen in die Ausgangsgleichung gibt $$x_{1,2} = 5 \pm \frac{45}{17} \sqrt{17}$$Einsetzen in die Gleichung für \(y\) gibt die Y-Koordinate von \(C\).

Jetzt bestimme die Nullstelle der Geraden mit der Steigung 1 (45°), die durch \(C\) verläuft - das ist \(g\). Dann hast Du die X-Koordinate von \(S\).

---

Die Lösung in Desmos:

die lilane Gerade ist \(g\). Der grüne Punkt ist \(C\) und der schwarze \(S\). Klick auf den 'Desmos'-Schriftzug rechts unten, dann siehst Du auch die Details.