Liebe Lounge,
eine Frage zur Definition des Tangens am Einheitskreis.
Zunächst einmal, als Voraussetzung darf die Definition des Sinus und des Cosinus am Einheitskreis benutzt werden.
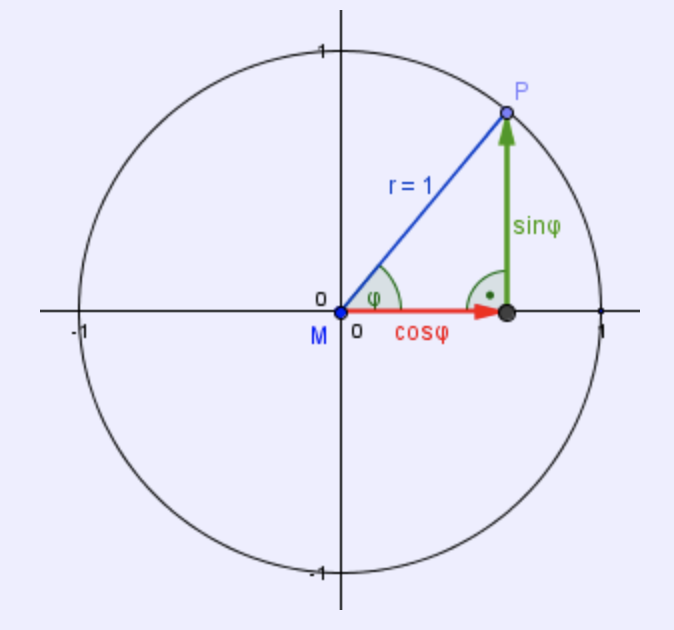
Dabei ist der Sinus des Winkels gerade die y-Koordinate von P und der Kosinus des Winkels gerade die x-Koordinate von P.
Jetzt wäre eine Möglichkeit, die ich nachvollziehen kann: Der Tangens für Winkel von 0-90° ist ja definiert als GK/AK. Wenn man das jetzt auf eine allgemeinere Ebene anheben will, also für Winkel größer 90°, wäre es logisch zu sagen: tan(phi)=sin(phi)/cos(phi).
Jetzt wird in den meisten Büchern allerdings das Dreieck des Einheitskreises so verändert, dass die Ankathete die Länge eins hat. Demnach gilt dann tan(phi)=GK/AK=GK/1=GK.
Das finde ich eigentlich noch intuitiver. Jetzt kommt allerdings die Stelle, an der es bei mir hakt:
Wieso ist, bei dieser letzten Betrachtungsweise, der tan(phi) mit 90°<phi<180° negativ? Das will sich mir auch mit graphischer Illustration nicht so ganz erschließen.
Deshalb zwei Fragen an euch:
1. Ist meine Herleitung/ Definition auch fein?
2. Kann mir jemand meine Frage zur geometrischen Deutung beantworten :)?
Vielen Dank, einen schönen Tag.
Euer Kombi!