Hallo,
interessante Frage, die gar nicht so leicht zu beantworten ist. Ich habe folgenden Erklärungsvorschlag:
Man definiert bei einem Dreieck ein Innen und Außen. Innen ist anschaulich alles, was sich innerhalb der Dreiecksfläche befindet. Also im Bild die grün markierte Fläche:
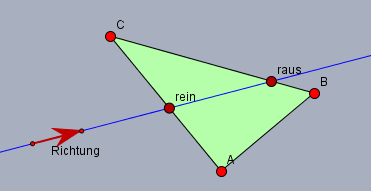
Weiter kann ich der Geraden (blau) eine Richtung zuweisen. Denkt man sich einen Punkt auf der Geraden, der in der definierten Richtung entlang der Geraden wandert, so muss dieser zwansgläufig alle Schnittpunkte der Geraden mit den Seiten des Dreiecks erreichen, da er ja auch alle Punkte der Geraden erreicht.
Erreicht er die erste Seite (oben CA), so gibt es einen Übergang von außen nach innen. Erreicht er eine weitere Seite, so gibt es es zwangsläufig einen Übergang von innen nach außen. Weil er lt. Vorgabe nie eine Ecke des Dreiecks trifft, ist dieser Übergang immer eindeutig.
Da sich der gedachte Punkt auf der Gerade im unendlichen garantiert immer außen befindet, muss die Anzahl der Schnittpunkte immer gerade sein. Und da ein und dieselbe Seite nur genau einmal geschnitten werden kann (zwei Geraden haben maximal genau einen Schnittpunkt), sind nur zwei Schnittpunkte mit zwei Seiten möglich, weil das Dreieck nur drei und nicht vier oder mehr Seiten hat.