Konvergenz von Reihen mit Quotientenkriterium

Question

Text erkannt:

\( 1=0 \) leanvergiest

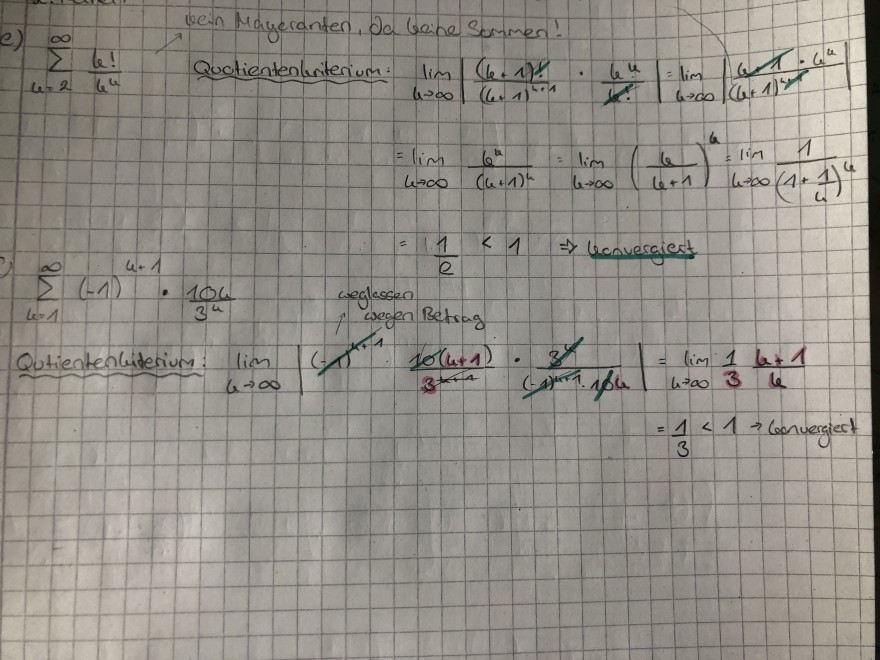
Meine Frage ist wie man von (k/k+1)^k auf 1/(1+1/k)^k kommt (Aufgabe e)

(Es geht um die Konvergenz von Reihen, mithilfe des Quotientenkriteriums)

Text erkannt:

bein Mayeranten, Da Geine Summen!
\( =\frac{1}{3}<1 \rightarrow \) convergiect

Answer 1

Aloha :)

Mir springt bei sowas immer sofort der Kehrwert in den Kopf. Ich schreibe das mal ausführlich auf, aber im Prinzip ist das ein Rechenschritt:$$\left(\frac{k}{k+1}\right)^k\;\;\stackrel{\text{(Kehrwert)}}{=}\;\;\left(\frac{k+1}{k}\right)^{-k}=\frac{\left(\frac{k+1}{k}\right)^{-k}}{1}\;\;\stackrel{\text{(Kehrwert)}}{=}\;\;\frac{1}{\left(\frac{k+1}{k}\right)^{k}}$$$$=\frac{1}{\left(\frac{k}{k}+\frac{1}{k}\right)^{k}}=\frac{1}{\left(1+\frac{1}{k}\right)^{k}}$$In meinem Kopf sieht das dann so aus:$$\left(\frac{k}{k+1}\right)^k=\frac{1}{\left(\frac{k+1}{k}\right)^k}$$Diese Art von "Doppel-Kehrwert" hilft bei erstaunlich vielen Umformungen weiter.

Comments

Danke für deine ausführliche Hilfe!

Answer 2

Hallo,

Klammere im Nenner k aus:

k+1= k(1 +1/k) und kürze dann k