Schnittfläche und -volumen zweier unterschiedlich großer Zylinder?

Question

Aufgabe: Schnittfläche und -volumen zweier Zylinder

ich möchte die Schnittfläche und das Schnittvolumen zweier Zylinder berechnen.

Zur Veranschaulichung.

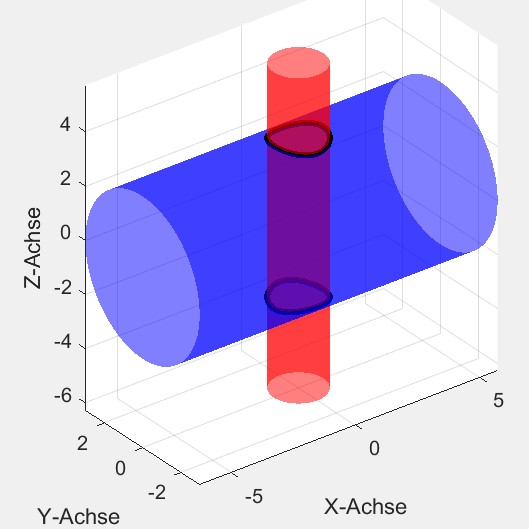
Der große, blaue Zylinder (u₁, v₁) R=3 liegt auf der x-Achse, der rote, kleine Zylinder(u₂, v₂) r=1 liegt auf der z-Achse, die Zylinder schneiden sich also. Um die Schnittkurve zu berechnen habe ich die Zylinder in Parameterform dargestellt und diese gleichgesetzt. Dabei habe ich alles nach u₂ umgeformt und dieses durch t ersetzt.

Formel der Schnittkurve

x=r•cos(t)

y=r•sin(t)

z=sqrt[R²-r²•sin(t)²]

Problem/Ansatz:

Für die Schnittfläche möchte ich ein Doppelintegral benutzen. Dabei nutze ich die erste Fundamentalform E, F und G. Beim Zylinder ist E=r², F=0 und G=1. Jetzt hänge ich aber bei den Integrationsgrenzen. Als erste Grenze möchte ich eine Funktion u(v) einsetzen, um die Kurve des kleinen Zylinders auf dem Großen abzubilden. Als zweite bin ich mir nicht sicher, entweder 0 bis 2•r oder 0 bis 2•π. Wie komme ich auf die Grenzen für die Schnittfläche?

Bei dem Schnittvolumen habe ich das gleiche Problem. Ich möchte ein Dreifachintegral nutzen, weiß aber nicht in welchen Grenzen.