Komplexe Integrale berechnen

Question

1) \( \int \limits_{C_{1}} \frac{1}{z^{2}} \mathrm{~d} z \)

2) \( \int \limits_{C_{2}} \sin (z) \cos (z) \mathrm{e}^{\sin ^{2}(z)} \mathrm{d} z \)

3) \( \int \limits_{C_{3}} \mathrm{e}^{z^{2}} \mathrm{~d} z \)

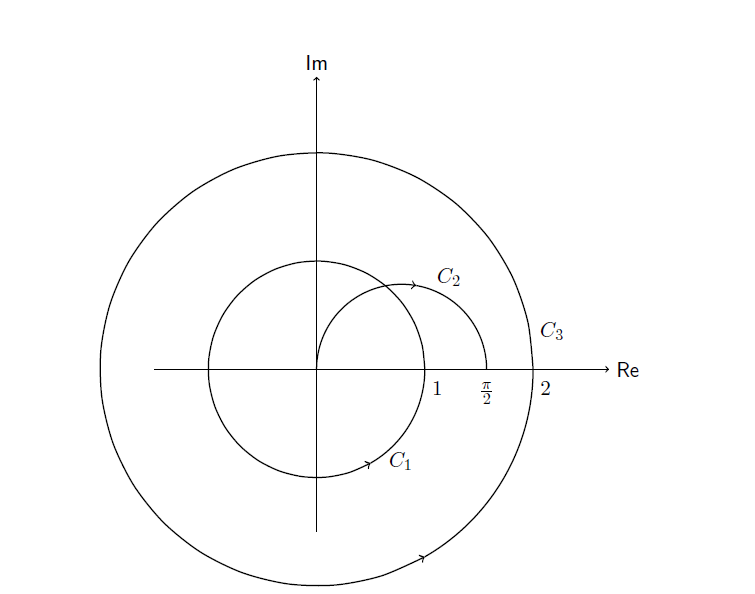
Ich soll die komplexen Integrale anhand der Abbildung berechnen.

Comments

meine Idee:
zu a)
$$\int_{C_{1}}^{} \! \frac{1}{z^2} \, dx = 0$$
C_1 scheint |z| = 1 zu sein. Aber das ist in diesem Fall egal, da f holomorph ist glaub ich. ich weiß nicht ob das hier relevant ist. aber wenn ja dann solche das ergebnis 0 sein



zu c) auch 0 wie a) mit c_3: |z| = 2 aber bin mir auch hier nicht sicher.

vielleicht können die Profis im Forum uns aufklären?