Flächeninhalt 2 Rechtecke in einer Funktion

Question

Aufgabe:

Marginalanalyse Fläche von 2 Rechtecken

Problem/Ansatz:

Text erkannt:

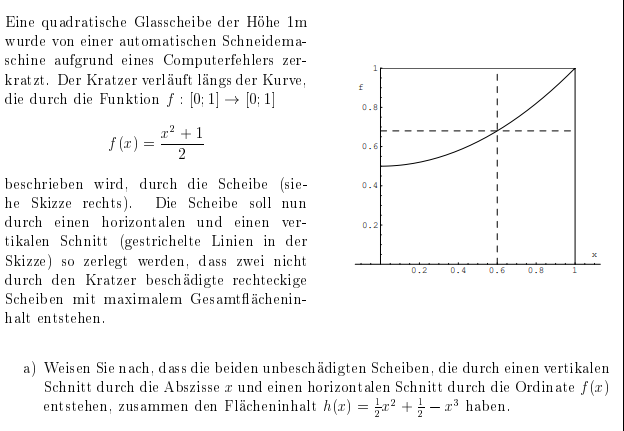
Eine quadratische Glasscheibe der Höhe \( 1 \mathrm{~m} \) wurde von einer aut omatischen Schneidemaschine aufgrund eines Computerfehlers zerkratzt. Der Kratzer verläuft längs der Kurve, die durch die Funktion \( f:[0 ; 1] \rightarrow[0 ; 1] \)
\( f(x)=\frac{x^{2}+1}{2} \)
beschrieben wird, durch die Scheibe (siehe Skizze rechts durch einen horizontalen und einen vertikalen Schnitt (gestrichelte linien in der Skizze so zerlegt werden, dass zwei nicht durch den Kratzer beschädigte rechteckige Scheiben mit maximalem Gesamtflächenin-
halt entstehen.
a) Weisen Sie nach, das s die beiden unbesch ädigten Scheiben, die durch einen vertikalen Schnitt durch die Abszisse \( x \) und einen horizont alen Schnitt durch die Ordinate \( f(x) \) ent stehen, zusammen den Flächeninhalt \( h(x)=\frac{1}{2} x^{2}+\frac{1}{2}-x^{3} \) haben.

Hallo, ich verstehe nicht ganz woraus sich die Funktion h(x) zusammensetzt bzw. wie man das hier berechnen soll.

Answer 1

Hallo,

ich verstehe nicht ganz woraus sich die Funktion h(x) zusammensetzt

schau Dir bitte folgendes Bild an:

https://jsfiddle.net/WernerSalomon/sedq10fx/14/

Der Kratzer auf der Scheibe läuft entlang der Parabel (blau). Nun wählt man eine Position \(x=|AX|\) an der man die Scheibe teilt und kann dann die beiden Rechtecke \(XBEY\) und \(HYGD\) (grün) herausschneiden. Die Summe \(F\) der beiden Flächen ist die Summe der Flächen der Rechtecke - also$$F = |AX| \cdot |YG| + |XB| \cdot |XY|$$Wir wissen dass die Punkte \(G\) und \(B\) bei \(y=1\) bzw. \(x=1\) liegen. Und \(Y\) liegt bei \(Y(x;\,f(x))\) daraus folgt:$$\begin{aligned} F &= |AX| \cdot |YG| + |XB| \cdot |XY| \\  &= x(1-f(x)) + (1-x) f(x) \\ &= x - 2xf(x) + f(x) \\&= x - x(x^2+1) + \frac 12(x^2+1) \\ &= -x^3 + \frac 12 x^2 + \frac 12 \\ &= h(x)\end{aligned}$$Du kannst oben im Bild den Punkt \(X\) (weis) mit der Maus verschieben. Dabei ändert sich natürlich die Fläche der beiden Rechtecke. Der Punkt 'Fläche' gibt dabei die Größe; umso höher er steigt, desto größer ist die Fläche. Die Fläche erreicht ein Maximum, wenn man \(X\) auf die senkrechte rot gestrichelte Linie schiebt. Dies ist die Position \(x=1/3\).

Um das zu berechnen, leitet man \(h(x)\) ab und setzt die Ableitung zu \(0\):$$\begin{aligned} h(x) &= -x^3 + \frac 12 x^2 + \frac 12 \\ h'(x) &= -3 x^2 + x \\ 0 &= x(-3 x + 1) \\ \implies x_1 &= 0, \quad x_2 = \frac 13\end{aligned}$$Die zweite Ableitung ist \(h''(x)= -6x+1\) und damit ist \(h''(\frac 13) \lt 0\). Also stellt sich das Maximum der Fläche bei \(x=1/3\) ein.

Answer 2

f(x) = 0.5·x^2 + 0.5

h(x) = x·(1 - f(x)) + (1 - x)·f(x) = - x^3 + 0.5·x^2 + 0.5

h'(x) = x - 3·x^2 = 0 → x = 0 oder x = 1/3

h(1/3) = 14/27 = 0.5185 m²