Hallo,
Willkommen in der Mathelounge!
Jetzt weiß ich leider nicht, wie ich auf den Winkel ... geschweige denn auf die Richtung r komme
Dann hast Du wahrscheinlich noch nie was von der Gauß'schen Zahlenebene gehört - oder? Aber Du weißt sicher, dass man die Zahlen (also die reellen Zahlen!) auf der Zahlengerade darstellen kann. Kommen die imaginären Zahlen hinzu, so wird aus dieser Geraden eine Ebene:
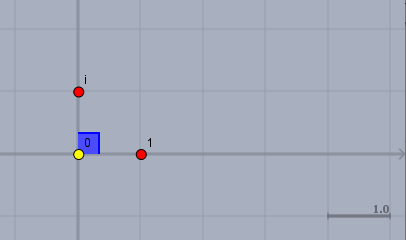
Der gelbe Punkt sei die \(0\) und der rote rechts daneben ist die \(1\). Beide liegen zusammen mit den anderen reellen Zahlen auf der Zahlengeraden (die graue Wagerechte). Die Zahl \(i\) liegt außerhalb, nämlich direkt oberhalb der \(0\). Und der Winkel, den der Ortsvektor zu \(i\) gegenüber der Zahlengeraden einnimmt, ist zwangsläufg \(90°=\pi/2\).
Also ist$$z = \sqrt{-81} = \sqrt{81} \cdot \sqrt{-1} = 9i = 9 \cdot e^{\frac{\pi}{2}i}$$Analytisch kommst Du da auch hin, wenn Du weißt, dass immer gilt$$\begin{aligned} r \cdot e^{\varphi i} &= r(\cos(\varphi) + i \cdot \sin(\varphi)) \\ &= \underbrace{r \cdot \cos(\varphi)}_{=0} + i \underbrace{\cdot r \cdot\sin(\varphi)}_{=9} \end{aligned}$$Im Falle von \(\sqrt{-81}\) ist der Realteil \(=0\), also ist \(\cos(\varphi)=0\). Der Imaginärteil ist positiv also muss \(\varphi = \frac{\pi}2\) sein, da $$\cos\left( \frac{\pi}2\right) = 0, \quad \sin \left( \frac{\pi}2\right) = 1$$demnach ist hier$$ r \cdot \sin\left( \frac {\pi}2\right) = r = 9$$\(r\) ist der Betrag von \(z\) nicht die Richtung.