Wie kann ich die Zahl \sqrt{-81} in die Exponentialschreibweise der imaginären Zahlen umschreiben?

Question

Wie kann ich die Zahl $\sqrt{-81}$ in die Exponentialschreibweise der imaginären Zahlen umschreiben?

Guten Morgen ihr Lieben,

ich wollte bei euch einmal nachfragen, wie ich  $\sqrt{-81}$ in die Exponentialschreibweise umschreiben kann, da ich die 4. Wurzel von ihr ziehen möchte.

Mein Ansatz ist wie folgt: $\sqrt{-1}$ stelle ich als i dar. Daraus ergibt sich:

z = 81 * i, Jetzt weiß ich leider nicht, wie ich auf den Winkel $\varphi$, geschweige denn auf die Richtung r komme.

Es wäre cool, wenn ihr mir da weiterhelfen könntet!

Habt alle einen schönen Tag und startet gut ins Wochenende!

Answer 1

Hallo,

Willkommen in der Mathelounge!

Jetzt weiß ich leider nicht, wie ich auf den Winkel ... geschweige denn auf die Richtung r komme

Dann hast Du wahrscheinlich noch nie was von der Gauß'schen Zahlenebene gehört - oder? Aber Du weißt sicher, dass man die Zahlen (also die reellen Zahlen!) auf der Zahlengerade darstellen kann. Kommen die imaginären Zahlen hinzu, so wird aus dieser Geraden eine Ebene:

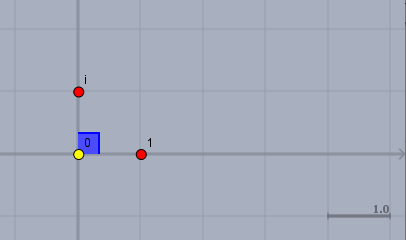
Der gelbe Punkt sei die $0$ und der rote rechts daneben ist die $1$. Beide liegen zusammen mit den anderen reellen Zahlen auf der Zahlengeraden (die graue Wagerechte). Die Zahl $i$ liegt außerhalb, nämlich direkt oberhalb der $0$. Und der Winkel, den der Ortsvektor zu $i$ gegenüber der Zahlengeraden einnimmt, ist zwangsläufg $90°=\pi/2$.

Also ist$$z = \sqrt{-81} = \sqrt{81} \cdot \sqrt{-1} = 9i = 9 \cdot e^{\frac{\pi}{2}i}$$Analytisch kommst Du da auch hin, wenn Du weißt, dass immer gilt$$\begin{aligned} r \cdot e^{\varphi i} &= r(\cos(\varphi) + i \cdot \sin(\varphi)) \\ &= \underbrace{r \cdot \cos(\varphi)}_{=0} + i \underbrace{\cdot r \cdot\sin(\varphi)}_{=9} \end{aligned}$$Im Falle von $\sqrt{-81}$ ist der Realteil $=0$, also ist $\cos(\varphi)=0$. Der Imaginärteil ist positiv also muss $\varphi = \frac{\pi}2$ sein, da $$\cos\left( \frac{\pi}2\right) = 0, \quad \sin \left( \frac{\pi}2\right) = 1$$demnach ist hier$$r \cdot \sin\left( \frac {\pi}2\right) = r = 9$$$r$ ist der Betrag von $z$ nicht die Richtung.

Comments

Vielen dank, die Erklärung war super und hat mir echt geholfen.

---

Vielen dank, die Erklärung war super und hat mir echt geholfen.

Prima - das freut mich :-)

Noch ein Hinweis. Man kann natürlich auch schon die $-81$ in Exponentialschreibweise schrieben: $$z^2 = -81 = 81 \cdot e^{\pi i}$$hier ist $r=81$, das ist der Betrag von $z$, und $\varphi=\pi$. Und Wurzelziehen bedeutet nun, die Wurzel aus dem (immer positiven) Betrag zu ziehen und den Winkel zu halbieren - und voila:$$z = \sqrt{81 \cdot e^{\pi i}} = 9 \cdot e^{\frac \pi2 i}$$