Cauchy-Produkt geometrischer Reihen

Question

Aufgabe:

Cauchy-Produkt

Problem/Ansatz:

Hallo :)

Kann mir jemand anhand der Aufgabe das cauchy-Produkt und die Vorgehensweise erklären?

Ich habe schon im Skript nachgeguckt und einige Videos geguckt, aber so richtig verstanden habe ich die Vorgehensweise und den Beweis noch nicht.

Danke für jede Hilfe :)

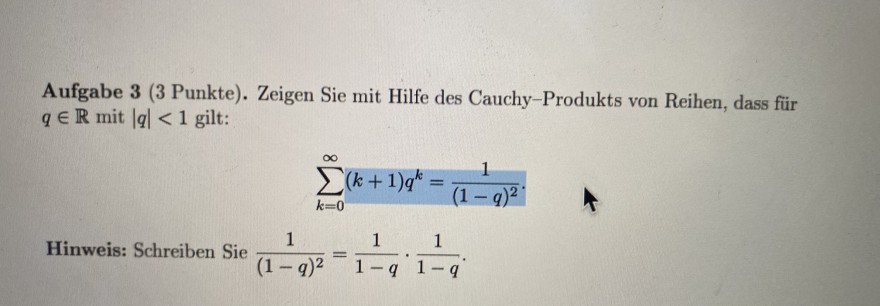
Text erkannt:

Aufgabe 3 ( 3 Punkte). Zeigen Sie mit Hilfe des Cauchy-Produkts von Reihen, dass für \( q \in \mathbb{R} \) mit \( |q|<1 \) gilt:
$$ \sum \limits_{k=0}^{\infty}(k+1) q^{k}=\frac{1}{(1-q)^{2}} $$
Hinweis: Schreiben Sie \( \frac{1}{(1-q)^{2}}=\frac{1}{1-q} \cdot \frac{1}{1-q} \)

Answer 1

Sei \(q\in \mathbb{R}\) und \(|q|<1\), dann gilt: $$\begin{aligned}\frac{1}{(1-q)^2}=\frac{1}{1-q}\cdot \frac{1}{1-q} \overset{(*)}=\left(\sum_{k=0}^{\infty}{q^k}\right)\cdot \left(\sum_{k=0}^{\infty}{q^k}\right)\overset{(\#)}=\sum_{k=0}^{\infty}{\sum_{m=0}^{k}{q^m\cdot q^{k-m}}} \\ = \sum_{k=0}^{\infty}{\sum_{m=0}^{k}}q^k=\sum_{k=0}^{\infty}{\left(q^k\cdot \sum_{m=0}^{k}{1}\right)}=\sum_{k=0}^{\infty}{q^k(k+1)} \end{aligned}$$

In \((*)\) wird der Grenzwert der Partialsummenformel für die geometrische Reihe verwendet. In \((\#)\) wird das Cauchyprodukt verwendet.

Comments

Dankeschön!

Ist das jetzt schon alles was zu zeigen war ?

Und die Reihe ist dann absolut Konvergent oder?

---

Und die Reihe ist dann absolut Konvergent oder?

Die geometrische Reihe konvergiert absolut. Vielleicht ist noch der Satz von Mertens interessant für dich.