Bestimmen Sie die Funktion f(x), welche den Kurvenverlauf beschreibt

Question

Zwei Straßenenden sind durch die Halbgeraden \( g(x) \) für \( x \leq 0 \) und \( h(x) \) für \( x \geq 4 \) gegeben.

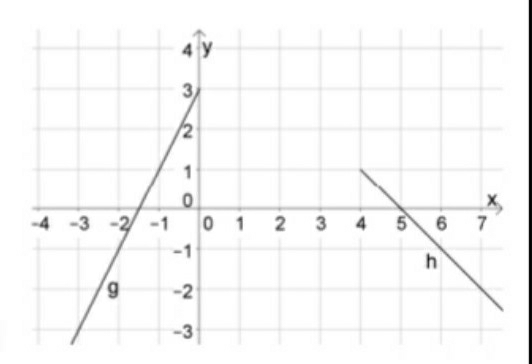
Sie sollen durch einen knickfreien Kurvenverlauf an den Stellen \( \mathrm{x}=0 \) und \( \mathrm{x}=4 \) miteinander verbunden werden. Der Einfachheit halber soll dieser Kurvenverlauf der Graph einer ganzrationalen Funktion \( \mathrm{f} \) mit möglichst kleinem Grad sein.

a) Stellen Sie die Geradengleichungen \( g(x) \) und \( h(x) \) auf? [zum Weiterrechnen: \( g(x)=2 x+3 \) und \( h(x)=-x+5] \)

b) Erläutern Sie, welche Konsequenz die Forderung des knickfreien Kurvenverlaufs für die Werte der 1. Ableitung \( f(x) \) an den Stellen \( x=0 \) und \( x=4 \) hat.

c) Bestimmen Sie die Funktion \( f(x), \) welche den Kurvenverlauf beschreibt.

d) Zeichnen Sie den Kurvenverlauf in das obige Diagramm ein.

Answer 1

Hilfe bei der Berechnung von Steckbriefaufgaben liefert die Seite:

http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Eigenschaften

f(0) = 3
f'(0) = 2
f(4) = 1
f'(4) = -1

Gleichungssystem

d = 3
c = 2
64a + 16b + 4c + d = 1
48a + 8b + c = -1

Lösung

f(x) = 0,125·x^3 - 1,125·x^2 + 2·x + 3

Skizze

Comments

Text erkannt:

\( (+\infty \)
kation
Symmetrie:
punktsymetrisch zu \( (3 \) I 2.25
Achsenschnittpunkte:
mit y-Achse: 3 mit \( x \) -Achse (Nullstellen):

Ich habe Eingenschaften eingegeben.Warum sieht der Graph bei mir so aus? Dankeschön für die Antwort im Voraus.

---

Das ist der Graph wie er über ganz R aussieht. Die Funktion gilt aber nur im Bereich von 0 bis 4. In den anderen Bereichen gelten die linearen Funktionen

---

Das habe ich jetzt verstanden!

Answer 2

1) P(0|3)

2) Q(4|1)

3) f '(0)=2

4) f '(4)=-1

Da 4 Bedingungen gegeben sind, ist der Ansatz:

f(x)=ax³+bx²+cx+d

und f'(x)=3ax³+2bc+c

1) bis 4) in diesen Ansatz einsetzen:

1) d=3

2) 1=64a+16b+4c+d

3) c=2

4) -1=48a+8b+c

Dies System hat die Lösungen: a=1/8, b=-9/8,c=2 und d=3.

Also: f(x)=1/8·x³-9/8·x²+2x+3

Comments

Vielen Dank!