Ich möchte den Winkel zwischen zwei Vektoren im Kreis zwischen 0 - 360 grad berechnen.

Question

Aufgabe: Ich möchte den WInkel zwischen zwei Vektoren aber nicht von 0-180 Grad sondern von 0 -360 Grad.

Problem/Ansatz: Ich hab recherchiert und den Ansatz gefunden.

Text erkannt:

Winkel zwischen zwei Vektoren - Formel

Das Problem ist, das die Formal nur einen Winkel von 0-180 Grad erlaubt. Ich suche aber eine die von 0-360 geht.

Falls mehr Informationen benötigt werden. Gerne mich wissen lassen.

Comments

Ich suche aber eine die von 0-360 geht.

Dazu müsstest du als erstes präzisieren, woran du erkennen willst, ob der Winkel

        φ mit 0° ≤ φ ≤ 180°

gesucht ist, oder der Winkel

        ψ = 360° - φ mit 180° < ψ < 360°?

---

Es geht um einen Kreis und den kann man sich folgendermaßen vorstellen. Da der Kreis 360 Grad besitzt, gehe ich davon aus, dass die WInkel zwischen 0 und 360 grad liegen. Ich möchte alle Winkel mit der Formel bestimmen z.b Winkel zwischen e und v und v und u etc....

Allerdings wird der Vektor e mit 0 grad beschrieben und dann in Uhrzeigersinn die Winkel bestimmt.

Ich kenne die Größe eines jeden WInkels aber nicht wie sie im Kreis liegen.
Es soll im Prinzip die Lage eines jeden Quaders im Kreis bestimmt werden zwischen 0 und 360 Grad.

Ich weiß es ist nicht ganz deutlich ich freue mich über Fragen.

Answer 1

Hallo,

Willkommen in der Mathelounge!

Ich möchte den WInkel zwischen zwei Vektoren aber nicht von 0-180 Grad sondern von 0 -360 Grad.

Berechne dazu sowohl den Cosinus, wie Du es bereits getan hast, als auch den Sinus des Winkels. Es ist:$$ \vec u \times \vec v = \left( |\vec u| \cdot |\vec v| \cdot \sin(\varphi) \right) \vec n$$Im 2-dimensionalen kannst Du das Kreuzprodukt interpretieren als$$\vec u \times \vec v = \left| \begin{array}{} u_x& v_x \\ u_y & v_y\end{array}\right| = u_x\cdot v_y - u_y \cdot v_x$$Anschließend benutzt Du die Funktion arctan2, die von den meisten Programmiersprachen und auch Tabellenkalkulationsprogrammen zur Verfügung gestellt wird. Da die Funktion arctan2(x,y) nur das Verhältnis berechnet (wie der Tangens), kannst Du schreiben:$$\varphi = \arctan2( \vec u \circ \vec v, \vec u \times \vec v )$$Achte darauf, dass das Ergebnis im Intervall \((-\pi; +\pi]\) bzw. \((-180°;\, +180°]\) liegt. Der Winkel ist stets der Winkel von \(\vec u\) nach \(\vec v\) in mathematisch positiver Richtung - also gegen den Uhrzeigersinn.

Siehe auch diese Frage. Und falls etwas unklar ist, so melde Dich noch einmal.

Gruß Werner

Comments

danke das ist super

---

Funktionert das auch, wenn der Kreis sein Mittelpunkt nicht im Ursprung hat? Weil der arctan2 geht doch immer von der x-Achse aus oder?

---

Funktionert das auch, wenn der Kreis sein Mittelpunkt nicht im Ursprung hat?

Ja - es wird ja nicht irgendein Winkel im Kreis, sondern ein Winkel zwischen zwei Vektoren berechnet. Liegt der Kreis z.B. bei \(M(3|\,1)\) und hat den Radius \(5\) und Du willst den Winkel zwischen den Vektoren \(\vec u\) (blau) und \(\vec v\) (rot) berechnen, die vom Mittelpunkt \(M\) zu den Punkten \(U\) und \(V\) zeigen,

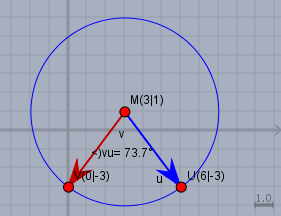
so musst Du natürlich zunächst die Differenz zu \(M\) bestimmen:$$\vec u = U - M = \begin{pmatrix}3\\ -4\end{pmatrix} \\ \vec v = V - M = \begin{pmatrix}-3\\ -4\end{pmatrix}$$Dann ist $$\vec u \circ \vec u = 7 \\ \vec u \times \vec v = -24$$Somit ist \(\varphi\) mit dem arctan2:$$\varphi = \arctan2 (7, -24) \approx -1,287 \approx -73,74° = 286,26°$$

Answer 2

Ich gehe eiinmal von den Vektoren
( x | y ) ( 4 | 3 ) und ( 1 | 7 ) aus
tan ( a1 ) = 3 / 4 = 0.75 = 36.87 °
tan ( a2 ) = 7 / 1 = 7 = 81.87  °
Der Unterschied = ( 81.87 ° - 36.87 ° ) = 45 °
( mit dem Uhrzeigersinn )

Du könntest auch -315 °
( gegen den Uhrzeigersinn )

nehmen.