Aufgabe:
Die folgende Abbildung zeigt eine geplante Hängebrücke. Aufgrund statischer Berechtigen Abstand angeordnete senkrechte Hängeseile an den hoiden Hom gleichen gegenseitigt wird. Die tiefsten Punkte der Haupttrageseile sollen sich jeweils 8 m über der Fahrler (Pylone), die sogenannte Spannweite der Brücke, beträgt laut Plan 160 m.
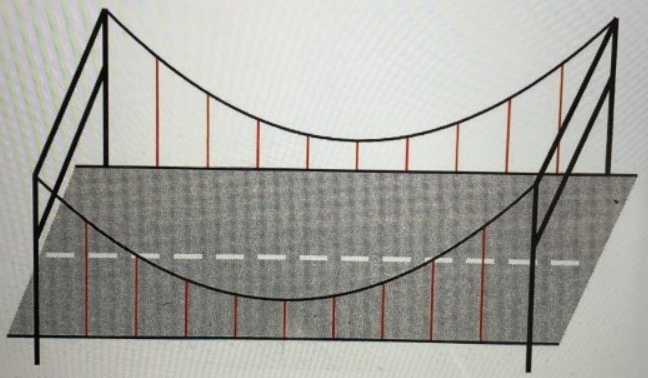
Das zuständige Bauingenieursbüro muss u. a. die Länge der Hängeseile bestimmen.
Hinweise :
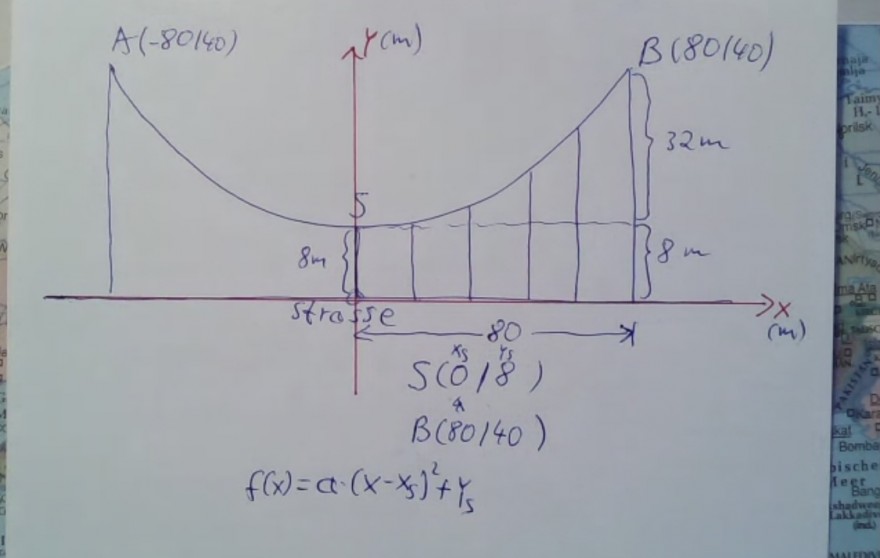
- Lege zunächst ein Koordinatensystem fest. Wähle den Usprung möglichst günstig.
- Bestimme bezüglich des gewählten Koordinatensystems die zu einem Haupttrageseil gehörende Funktionsgleichung. Beachte: Liegt ein Punkt \( P\left(x_{p} / y_{P}\right) \) auf der Kurve, so gilt : \( f\left(x_{p}\right)=y_{p} \). Durch Einsetzen der Koordinaten markanter Punkto erhält man Bestimmungsgleichungen für die unbekannten Parameter der Funktionsgleichung.
Wie lang sind die Hängeseile?
Ansatz: