Aufgabe:
Die folgende nicht maßstäbliche Skizze (Abb.1) zeigt einen Teil einer Überlandleitung, die zwischen gleich hohen Masten in einem ebenen Gelände aufgespannt ist. Unter der Leitung befindet sich in einem gewissen Sicherheitsabstand ein Wohnhaus:
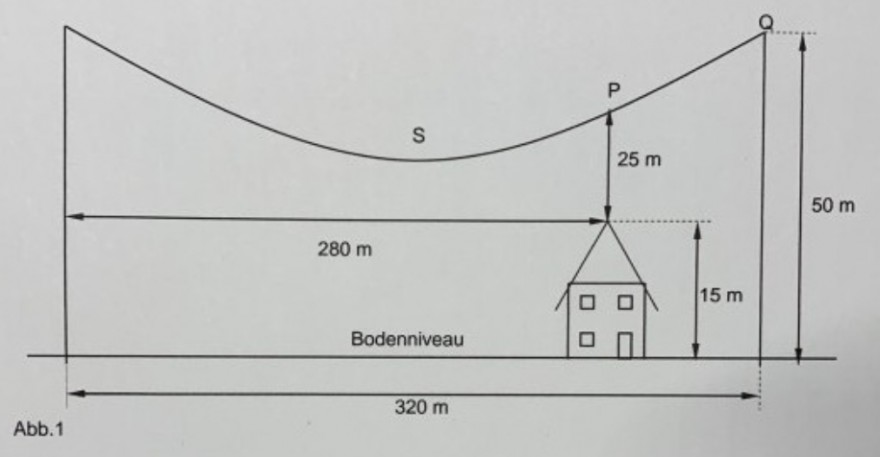
Die Wipfel von Bäumen, welche im Bereich unter der Leitung wachsen, müssen einen vertikalen Mindestabstand von 2 m zur Leitung haben. Wie hoch dürfen die Bäume im Bereich des bodennächsten Punkts S der Leitung höchstens werden? (Rundung auf m)
Entnimm die dazu benötigten Maße der Skizze. Gehe davon aus, dass die Leitung in Form einer Parabel durchhängt. (Physikalische Betrachtungen zeigen, dass dies nicht ganz stimmt.) Bestimme nach Wahl eines geeigneten Koordinatenursprungs zunächst die Parabelgleichung.
Versuche zunächst eine eigenständige Lösung ohne die Hinweise auf der folgenden Seite.---
Lösungshinweise:
Lege den Ursprung des Koordinatensystems senkrecht unter S auf das Bodenniveau. Setze die Scheitelpunktform (SPF) an. Eine Koordinate von S ist bekannt.
Die SPF enthält noch die beiden Unbekannten a und \( y_{s} . \) Setzt man jeweils die (aus den Maßen der Abb. 1 zu bestimmenden) Koordinaten der Punkte \( P \) und \( Q \) ein, so erhält man ein lineares Gleichungssystem (LGS) mit zwei Gleichungen für diese Unbekannten. Das LGS kann nach einer der bekannten Methoden gelöst werden (möglichst von Hand, zur Not bzw. zur Kontrolle mit dem entsprechenden Menü des TR).
Zwerg. : \( \left.\mathrm{a}=\frac{1}{1120} ; \mathrm{y}_{\mathrm{s}}=\frac{190}{7}\right) \)
Anhand der Funktionsgleichung lässt sich nun die eigentliche Frage leicht beantworten.