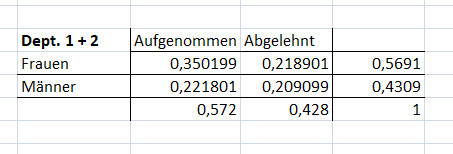
a. Wie groß ist die Wahrscheinlichkeit (in Prozent), dass eine Bewerbung an der Universität von einer Frau eingereicht wird und nicht erfolgreich ist?
Frauen ∩ Abgelehnt
b. Wie viel Prozent der Bewerber/innen insgesamt sind männlich?
Summe der rechte Spalte, mittlere Zeile
c. Wie groß ist die Wahrscheinlichkeit (in Prozent), dass ein Mann an der Universität nicht aufgenommen wird?
\(P_M(Abgelehnt)=\frac{0,209099}{0,4309}\)
d. Wie groß ist die Wahrscheinlichkeit (in Prozent), dass eine erfolglose Bewerbung an der Universität von einem Mann eingereicht wurde?
\(P_{Abgelehnt}(M)=\frac{0,209099}{0,428}\)