Hallo Leonie,
Hat jemand vielleicht eine Skizze ich kann mir das nicht vorstellen
Wichtigster Tipp dazu: versuche selber eine Skizze zu erstellen, das übt. So eine wie diese:
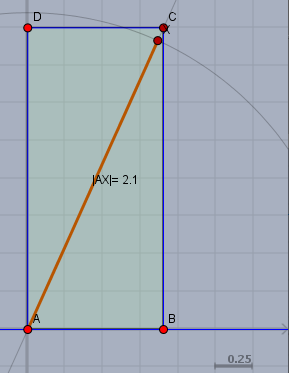
Die Türöffnung soll das markierte Rechteck \(ABCD\) sein. Die Breite \(|AB|=0,9\,\text m\) und die Höhe der Tür ist \(|BC| = 2\,\text m\). Wenn man die 4m lange Holzplatte auf die lange Seite stellt, so ist sie 2,1m hoch. Kippt man sie dann noch leicht zur Seite, in Richtung der Diagonalen der Tür, dann passt sie hindurch.
Die braun markierte Strecke \(|AX|=2,1\,\text m\) ist kürzer als die Diagonale \(|AC|\) der Tür . Das rechne ich noch mal nach. Das relevante Dreieck ist das Dreieck \(\triangle ABC\). Der rechte Winkel ist beim Punkt \(B\) und die Hypotenuse liegt gegenüber vom rechten Winkel, also der Diagonale \(|AC|\). Und die ist nach Pythagoras$$|AC| = \sqrt{|AB|^2 + |BC|^2} = \sqrt{2^2 + 0,9^2}\, \text m \approx 2,19\, \text m$$und das ist mehr als die \(2,1\,\text m\) der Holzplatte.
Gruß Werner