Umständliche Konstruktion eines Spiegelpunktes

Question

Zeichne eine Strecke CD sowie ihre Mittelsenkrechte m. Der Urpunkt M der Spiegelung an CD liege auf m. Zeichne eine Gerade g durch D, sodass das Lot von M auf g die Strecke CD nicht schneidet. Der Fußpunkt des Lotes von M auf g sei E. Der Kreis um E mit dem Radius |(ED) ̅ | schneidet g in A. Der Kreis um C mit dem Radius |(CA) ̅ | schneidet g in B. Die Mittelsenkrechte auf (DB) ̅ schneidet m in M‘. dann ist M‘ der Bildpunkt von M bei Spiegelung an CD. Beweise dies.

Answer 1

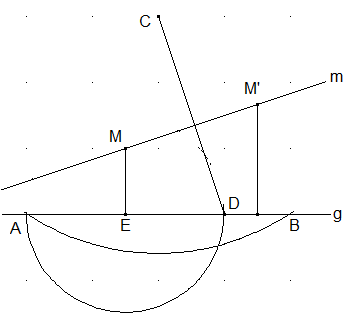
Ich benennen den Fußpunkt von C auf g mit F_C und den Fußpunkt von M' mit E', den Schnittpunkt S und den Fußpunkt davon F_S

F_S sei mein Koordinatenursprung

$$F_S =(0;0) ; E=(-a;0) ; E'=(a;0) ; D=(b;0) ; F_C=(-b;0) ; A=(-2a-b;0) ; B=(2a-b;0)$$

$$DE'=a-b=2a-b-a=E'B$$

Answer 2

Lösungsmöglichkeit mittels Koordinatenbestimmung

mfG

Moliets