Wächst die Fläche des Ölteppichs momentan?

Question

Aufgabe:

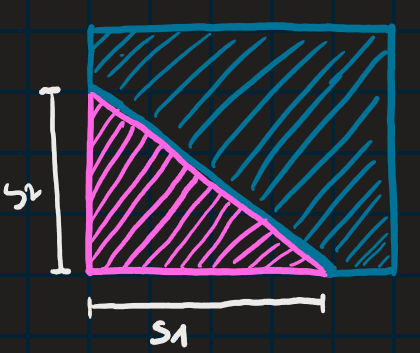
Die folgende Skizze zeigt einen Ölteppich in einer rechteckigen Bucht, dessen Abmessungen sich im Laufe der Zeit verändern, wobei der freie Rand des Ölteppichs jedoch gerade bleibt.

Momentan ist s1 25% Größer als s2 und s1 nimmt mit einer 20% geringeren Geschwindigkeit ab, als s2 zunimmt. Wächst die Fläche des Ölteppichs momentan?

Text erkannt:

A2-4-4.) Die folgende Skizze zeigt einen Ölteppich in einer rechteckigen Bucht, dessen Abmessungen sich im Laufe der Zeit verändern, wobei der freie Rand des Ölteppichs jedoch gerade bleibt.
Momentan ist \( s_{1} 25 \% \) größer als \( s_{2} \) und \( s_{1} \) nimmt mit einer \( 20 \% \) geringeren Geschwindigkeit ab, als \( s_{2} \) zunimmt. Wächst die Fläche des Ölteppichs momentan?

Text erkannt:

\( \frac{5 x}{110} \)

Problem/Ansatz:

Bisher kam ich auf Ansätze wie A(x) = sqrt(s1-0,8x)² + (s2 + x)²) mit s1 = 5/4 s2

Zusammengefasst sqrt(41/16 * s2² + 1,64x²)

Ich komme aber nicht wirklich weiter und bin mir bei dem Ansatz absolut nicht sicher.

Könnte jemand einen richtigen Ansatz nennen?

Comments

Deine Kathetenlängen sind richtig, allerdings berechnest du danach die Länge der Hypotenuse und nicht den Flächeninhalt des rechtwinkligen Dreiecks.

Answer 1

A(x) = 1/2·(1.25 + x)·(1 - 0.8·x) = 0.625 - 0.4·x^2

Damit würde die Fläche im folgenden abnehmen.

Comments

Damit würde die Fläche im folgenden abnehmen.

Wenn "damit" richtig wäre, dann wäre also auch die Abnahme richtig.

Answer 2

s1, s2 wie in der Grafik

aa = Ausgangsfläche
an = Fläche neu

Beispiel

Die Grafik zeigt das für x = 0 bis 3 die Fläche 31.25
zunimmt und dann wieder kleiner wird.
Steht vielleicht nicht in Überstimmung zur Meinung des
coaches.

Comments

Naja, der hat die funktion auch rauskehrt umbracht

>A(x) = 1/2·(1.25 + x)·(1 - 0.8·x)