Berechnen Sie die Anzahl der Besucher, die um 12 Uhr im Park sind.

Question

Aufgabe:

Text erkannt:

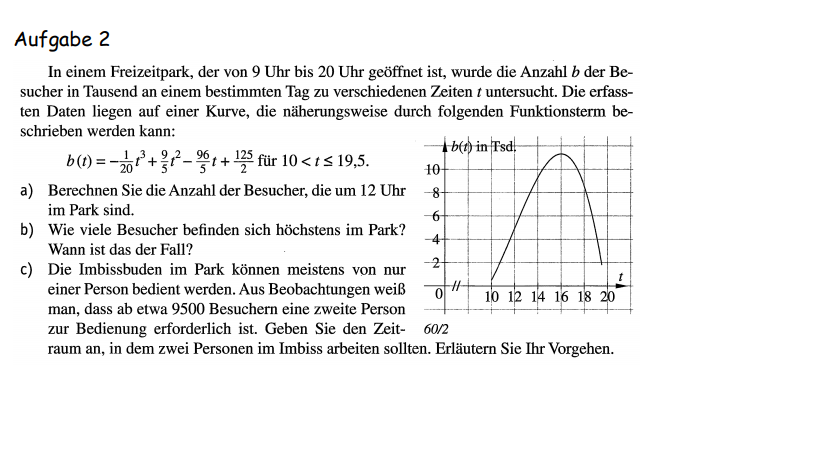
Aufgabe 2
In einem Freizeitpark, der von 9 Uhr bis 20 Uhr geöffnet ist, wurde die Anzahl \( b \) der Besucher in Tausend an einem bestimmten Tag zu verschiedenen Zeiten \( t \) untersucht. Die erfassten Daten liegen auf einer Kurve, die näherungsweise durch folgenden Funktionsterm beschrieben werden kann:
\( b(t)=-\frac{1}{20} t^{3}+\frac{9}{5} t^{2}-\frac{96}{5} t+\frac{125}{2} \) für \( 10<t \leq 19,5 \)
a) Berechnen Sie die Anzahl der Besucher, die um 12 Uhr im Park sind.
b) Wie viele Besucher befinden sich höchstens im Park? Wann ist das der Fall?
c) Die Imbissbuden im Park können meistens von nur einer Person bedient werden. Aus Beobachtungen weiß man, dass ab etwa 9500 Besuchern eine zweite Person zur Bedienung erforderlich ist. Geben Sie den Zeit- \( 60 / 2 \) raum an, in dem zwei Personen im Imbiss arbeiten sollten. Erläutern Sie Ihr Vorgehen.

Problem/Ansatz:

ich weiß nicht wie ich bei der Aufgabe vorgehen soll. Wie berechne ich diese Aufgaben?

Answer 1

a) t = 12 einsetzen

b) erste Ableitung gleich Null setzen, nach t auflösen, dieses t in die Funktion (nicht in die Ableitung) einsetzen

c) Funktion gleich 9,5 setzen. Die Lösungen geben die beiden t an, bei denen die zweite Person nötig wird bzw. nicht mehr nötig ist.

Comments

Das sieht etwa so aus:

---

Ist das für die Aufgabe c?

---

Die Graphik ist eigentlich für die gesamte Aufgabe nützlich.

Die t-Koordinaten der Schnittpunkte der Geraden mit b(t) sind die Lösungen für Teil c), ja.