Bild, Faser und Kern einer linearen Abbildung

Question

Könnte mir jemand zeigen wie man diese Aufgabe löst? Dankeschön!

Die Matrix

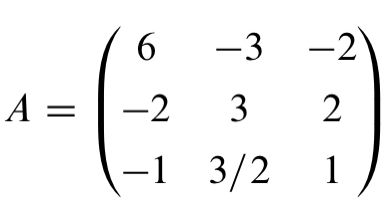
Text erkannt:

\( A=\left(\begin{array}{ccc}6 & -3 & -2 \\ -2 & 3 & 2 \\ -1 & 3 / 2 & 1\end{array}\right) \)

definiere den Endomorphismus \( f: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}, x \mapsto A x, \) vermöge des Matrixprodukts mit der Spalte \( x \)
a) Bestimmen Sie den Rang von \( f \) und die Dimension des Kerns. Finden Sie eine Basis \( A \) von ker \( f \)
b) Geben Sie einen Untervektorraum \( U \) an, so daß \( \mathbb{R}^{3}=U \oplus \) ker \( f \).
c) Finden Sie eine Basis \( \mathcal{B} \) von im \( f \), und begründen Sie, daß \( \mathcal{B} \) mit \( (0,0,1)^{\top} \) zu einer Basis des Wertebereichs \( \mathbb{R}^{3} \) wird.
d) Geben Sie für \( y \in \operatorname{im} f \) eine Parametrisierung der Faser \( f^{-1}(y) \) an. Hinweis: Benutzen Sie, daß jede nichtleere Faser \( f^{-1}(y) \) genau einen Schnittpunkt mit \( U \) hat. Bestimmen Sie zunächst diesen Schnittpunkt, also die Abbildung \( \varphi: \operatorname{im} f \rightarrow U, y \mapsto x \) mit \( \{x\}=f^{-1}(y) \cap U \).
e) Interpretieren Sie die bisher gefundenen Ergebnisse geometrisch.
f) Nach dem Faktorisierungssatz gibt es eine Projektion \( \pi: \mathbb{R}^{3} \rightarrow U, \) einen Isomorphismus \( \left.f\right|_{U}: U \rightarrow \operatorname{im} f \) und eine Injektion \( \iota: \operatorname{im} f \rightarrow \mathbb{R}^{3} \) mit \( f=\left.\iota \circ f\right|_{U} \circ \pi \)

Geben Sie (für Ihre Wahl von \( U \) ) Matrixdarstellungen \( P \in \mathbb{R}^{2 \times 3}, F \in \mathbb{R}^{2 \times 2} \) und \( J \in \mathbb{R}^{3 \times 2} \) von \( \pi,\left.f\right|_{U} \) bzw. \( \iota \) in geeigneten Basen an. Überprüfen Sie, \( \operatorname{daB} A=J F P \). Vorsicht: ker \( f \) ist im allgemeinen nicht orthogonal \( \operatorname{zu} U, \) damit ist die Projektion \( \pi \) keine orthogonale Projektion.

Answer 1

a) Der Rang von \(f\) ist dere Rang von \(A\).

Für den Kern von \(f\), löse die Gleichung \(Ax = 0\).

b) Ergänze die Basis des Kerns von \(f\) zu eineer Basis von \(\mathbb{R}^3\). Die Vektoren, die du dazu zusätzlichen in die Basis aufgenommen hast, sind eine Basis von \(U\).

c) Sei \(S\) die Menge der Spaltenvektor der Matrix \(A\).

Wähle aus \(S\) einen Vektor aus und stelle ihn als Linearkombination der anderen Vektoren aus \(S\) dar. Falls das funktioniert, dann entferne ihn aus \(S\).

Wiederhole bis du alle Vektoren aus \(S\) so behandelt hast.

Was übrig bleibt ist eine Basis von \(\operatorname{im} f\).