Integralrechnung mithilfe von Transformationen

Question

Ich soll folgende Aufgabe lösen und ich komme nicht so wirklich klar damit.
Könnte mir einer dabei helfen bitte:

Benutzt die Transformationen, um die folgenden Integrale zu berechnen. Zeichnet auch die Integrationsgebiete vor und nach der Transformation.
$$\int_{0}^{1} \int_{0}^{1-x} \sqrt{x+y}(y-2 x)^{2} \mathrm{~d} y \mathrm{~d} x \text { mit } u=x+y \text { und } v=y-2 x$$

Ich weiß nicht was ich damit anfangen soll.

Answer 1

Hallo,

vor der Transformation handelt es sich um ein dreieckiges Integrationsgebiet mit den Eckpunkten \((0,0)\), \((1,0)\) und \((0,1)\). Es handelt sich bei \(\Phi\) um einen Diffeomorphismus (Prüfe Funktionaldeterminante):$$\Phi : \begin{pmatrix} u\\v \end{pmatrix}\mapsto \begin{pmatrix} x+y\\y-2x \end{pmatrix}=\underbrace{\begin{pmatrix} 1 & 1 \\ -2 & 1 \end{pmatrix}}_{=:A}\begin{pmatrix} x\\y \end{pmatrix}$$ \(A\) ist die Abbildungsmatrix. Multiplizierst du die Eckpunkte mit der Matrix, so hast du die Eckpunkte des neuen Integrationsbereichs bestimmt. In einem \(u-v\)-Koordinantensystem sieht das natürlich anders aus.

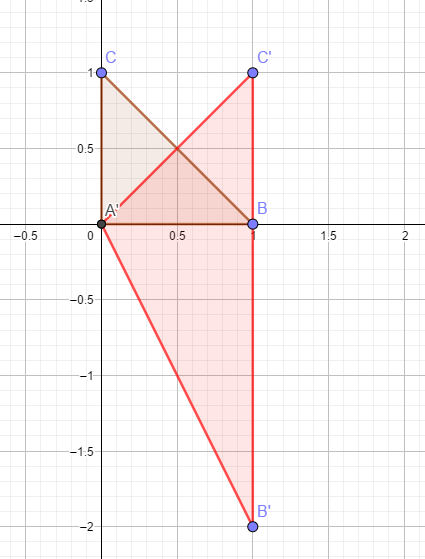
Nun wendet man den Transformationssatz an.