a)
Eine Pyramide und ein Kegel haben dann das gleiche Volumen, wenn ihre Grundfläche und ihre Höhe gleich groß sind.
Stelle beide Körper mit der Spitze unten auf den Tisch. Die Pyramide sei der Einfachheit halber eine quadratische Pyramide.
Zuunterst haben beide Körper die Fläche 0 und zuoberst (Höhe H) gilt nach Voraussetzung
πR^2 = A^2
Nun ein Schnitt auf einer Höhe h über dem Tisch: πr^2 resp. a^2. Man muss begründen, dass die beiden Schnittflächen gleich sind.
Nach dem 2. Strahlensatz gilt im Kegel R/H = r/h ==> Rh/H = r.
In der Pyramide: A/H = a/h ==> Ah/H = a
Daher πr^2 = πR^2 h^2/H^2
und a^2 = A^2 h^2/H^2
πr^2 = πR^2 h^2/H^2 = ?= a^2 = A^2 h^2/H^2
πR^2 h^2/H^2 = A^2 h^2/H^2 |*H^2, : h^2
πR^2 =?=A^2 was nach Voraussetzung der Fall ist.
Daher gilt: πr^2 resp. a^2 qed a)
b)
Eine Halbkugel mit Radius R hat das gleiche Volumen wie der Restkörper, der aus einem Zylinder mit Radius R und Höhe R gebildet wird, aus dem man einen Kegel mit Radius R und Höhe R entfernt.
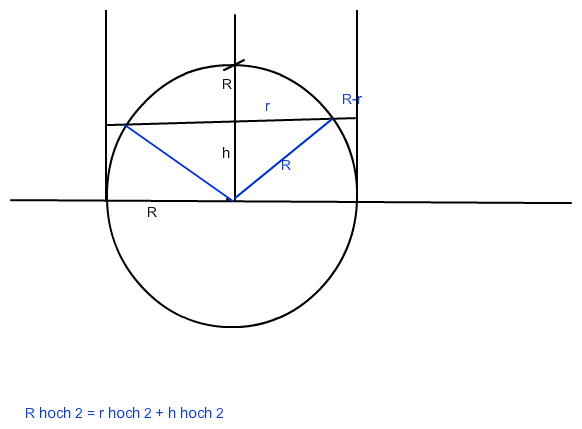
In meiner Skizze sind die gegebenen Körper mit Grossbuchstaben bezeichnet. Schnittfiguren: Kleine Buchstaben kommen ins Spiel.
Nun ist zu zeigen, dass der Ring der Breite R-r auf der Höhe h die gleiche Fläche hat wie oben.
Also: Da H=R. Behauptung: Fläche(Ring) = πR^2 h^2/R^2 = π h^2.
)