Berechnung der Profilline des oberen Bogens einer Vase, Funktion 3. Grades.

Question

Aufgabe:

Eine 20cm hohe Vase hat in 3,5cm Höhe ihren größten Durchmesser mit 11,6cm und in 14cm Höhe ihre schmalste Stelle mit einem Durchmesser von 5,4cm.

Nr.1a)

Legen Sie ein Koordinatensystem so, dass die x-Achse in der Symmetrieachse der Vase liegt und der Ursprung in der Mitte des Bodens der Vase. Berechnen sie eine ganzrationale Funktion dritten Grades, deren Graph die Profillinie des oberen Bogens der Vase bschreibt.

Problem/Ansatz:

Ich schaffe es gar nicht erst genug Bedingungen zu finden. Ich kann mir vorstellen, dass links und rechts an den Rändern jeweils ein Hochpunkt ist, wo die Höhe 20cm beträgt. Aber kann ich mir nicht vorstellen, wie man den Bogen oben ermitteln kann. Also bräuchte ich paar Tipps wie man hier vorgehen muss.

Vielen Dank!

Answer 1

Ist vielleicht nur das richtige Einzeichnen ins Koordinatensystem das Problem ?

Zeichnen wir (wie üblich) die x-Achse nach rechts, so hat man eben die Vase für die Beschreibung "flachgelegt" ...

Als Graph (obere Randkurve) ergibt sich dann eine kubische Parabel mit dem Hochpunkt H(3.5|5.8)  und dem Tiefpunkt  T(14|2.7)  (Radius = halber Durchmesser). In der Kurvengleichung hast du 4 Parameter a,b,c,d. Du brauchst entsprechend auch 4 Bedingungen. Siehst du jetzt, welche ?

Comments

Ja wenn man Hoch- und Tiefpunkt hat, dann kann man ja daraus 4 Bedinugnen nehmen. Dankeschön, ich kam irgendwie nicht so mit der Aufgabenstellung zurecht.

Answer 2

Eine 20cm hohe Vase hat in 3,5cm Höhe ihren größten Durchmesser mit 11,6cm und in 14cm Höhe ihre schmalste Stelle mit einem Durchmesser von 5,4cm.

90 ° gedreht
( x | y)
( 3.5 | 5.8 )
( 14 | 2.7 )
f ( 3.5 ) = 5.8
f ´( 3.5 ) = 0
f ( 14 ) = 2.7
f ´( 14 ) = 0

f ( x ) = a* x^3 + b * x^2 + c * x + d
f ´ ( x ) = 3 * a* x^2 + 2 * b * x + c

Comments

f(x) =
0,005355793111 * x^3 -
0,140589569161  *x^2 +
0,787301587302 * x +
4,537037037037

Answer 3

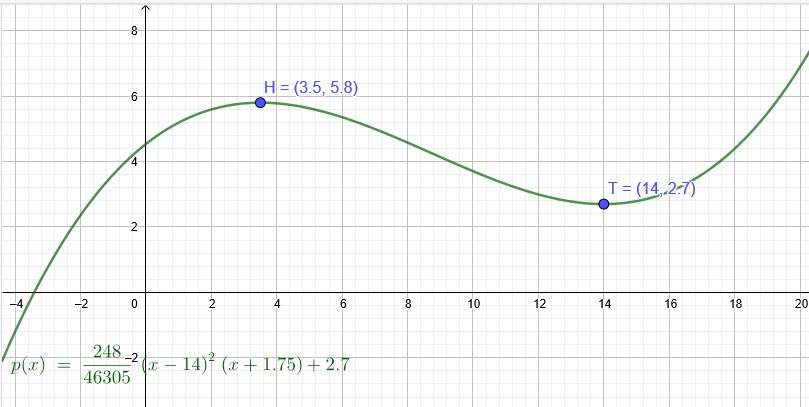
Polynomfunktion 3.Grades:

Maximum bei \(H(3,5|5,8)\)    und   Minimum bei \(T(14|2,7)\)
Graph verschieben um \(2,7\)↓:
Maximum bei \(H´(3,5|3,1)\)  und   Minimum bei \(T´(14|0)\) ist doppelte Nullstelle
\(f(x)=a[(x-14)^2(x-N)]\)
\(f'(x)=a[(2x-28)(x-N)+(x-14)^2]\)

\(H´(3,5|...)\):

\(f'(3,5)=a[(7-28)(3,5-N)+(3,5-14)^2]\)

\(a[(7-28)(3,5-N)+(3,5-14)^2]=0\)

\(N=-1,75\)

\(f(x)=a[(x-14)^2(x+1,75)]\)

\(H´(3,5|3,1)\):

\(f(3,5)=a\cdot(3,5-14)^2(3,5+1,75)=3,1\)

\(a =\frac{248}{46305}\)

\(f(x)=\frac{248}{46305}(x-14)^2(x+1,75)\)

Graph verschieben um \(2,7\)↑:

\(p(x)=\frac{248}{46305}(x-14)^2(x+1,75)+2,7\)