
Text erkannt:
Aufgabe 2 Konvergenz Für \( n \in \mathbb{N} \) sei \( X_{n} \) eine Zufallsvariable mit Dichtefunktion \( f_{n}(x)=n \cdot x^{n-1} \mathbb{1}_{[0,1]}(x) . \) Konvergiert die Folge \( \left(X_{n}\right)_{n \in \mathbb{N}} \) stochastisch?
Lösung:
o Die Dichte strebt für \( n \rightarrow \infty \) und \( x \in[0,1[ \) fix gegen Null: Regel von
$$ \text { l'Hôpital liefert } \frac{d}{d n}\left(\frac{n}{\frac{1}{x^{n-1}}}\right)=\frac{x^{n-1}}{-\log x} \stackrel{n \rightarrow \infty}{\longrightarrow} \frac{0}{-\log x}=0 $$
Nur für \( x=1 \) strebt die Dichte für \( n \rightarrow \infty \) nicht gegen Null.
Behauptung: \( \left(X_{n}\right)_{n \in \mathbb{N}} \) konvergiert stochastisch gegen 1
o Für \( \varepsilon>0 \) gilt
$$ \begin{aligned} \mathbb{P}\left(\left|X_{n}-1\right| \geq \varepsilon\right) &=\mathbb{P}\left(X_{n}-1 \geq \varepsilon\right)+\mathbb{P}\left(X_{n}-1 \leq-\varepsilon\right) \\ &=\mathbb{P}\left(X_{n} \leq 1-\varepsilon\right) \\ &=\int \limits_{0}^{1-\varepsilon} f(x) d x \\ &=\int \limits_{0}^{1-\varepsilon} n \cdot x^{n-1} d x \\ &=\left[x^{n}\right]_{0}^{1-\varepsilon}=(1-\varepsilon)^{n} \stackrel{n \rightarrow \infty}{\longrightarrow} 0 \end{aligned} $$
o Somit \( \lim \limits_{n \rightarrow \infty} \mathbb{P}\left(\left|X_{n}-1\right| \geq \varepsilon\right)=0 \) also \( X_{n} \stackrel{\mathbb{P}}{\rightarrow} 1 \)
Hallo Leute,
könnt ihr mir erklären,
1. wie kommt das 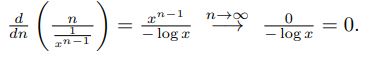
Text erkannt:
\( \frac{d}{d n}\left(\frac{n}{\frac{1}{x^{n-1}}}\right)=\frac{x^{n-1}}{-\log x} \stackrel{n \rightarrow \infty}{\longrightarrow} \frac{0}{-\log x}=0 \)
Ich habe gerechnet, dass die Ableitung von n.xn-1 = xn-1(log(x).n+1) gegen unendlich, wenn n -> unendlich.
2. Warum hier ist P (Xn < 1 - ε)? Warum nicht P(Xn > ε+1)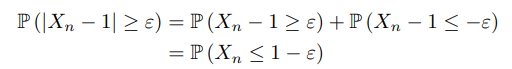
Text erkannt:
\( \begin{aligned} \mathbb{P}\left(\left|X_{n}-1\right| \geq \varepsilon\right) &=\mathbb{P}\left(X_{n}-1 \geq \varepsilon\right)+\mathbb{P}\left(X_{n}-1 \leq-\varepsilon\right) \\ &=\mathbb{P}\left(X_{n} \leq 1-\varepsilon\right) \end{aligned} \)
Vielen Dank.
LG ThomasMuller