Ab welchem Punkt ist die Tangente an den Graphen von f parallel zur Geraden g?

Question

Aufgabe:

In welchem Punkt P(x₀|f(x₀)) ist die Tangente an den Graphen von f parallel zur Geraden g mit g(x)=−x−2

f(x)=−x²−2


m=1

f '(x)=−x²−2

(f ' (x)=−2x−2 = −4 | wenn es richtig ist)



Komme ab hier nicht weiter.

Answer 1

Aloha :)

Die Gerade \(g(x)=-x-2\) hat die Steigung \((-1)\).

Die Steigung der Tangente an die Funktion \(f(x)=-x^2-2\) ist gleich \(f'(x)\).

Die Ableitung lautet \(f'(x)=-2x\).

Wir müssen also die Stelle \(x_0\) finden, bei der die Ableitung \(f'(x_0)\) gleich \((-1)\) ist.

$$-1\stackrel!=f'(x_0)=-2x_0\implies x_0=\frac{1}{2}$$Der gesuchte Punkt ist also \(\left(\frac{1}{2}\;;-\frac{9}{4}\right)\).

~plot~ -x^2-2 ; -x-2 ; -x-7/4 ; ; {1/2|-9/4} ; [[-2|2|-6|0]] ~plot~

Answer 2

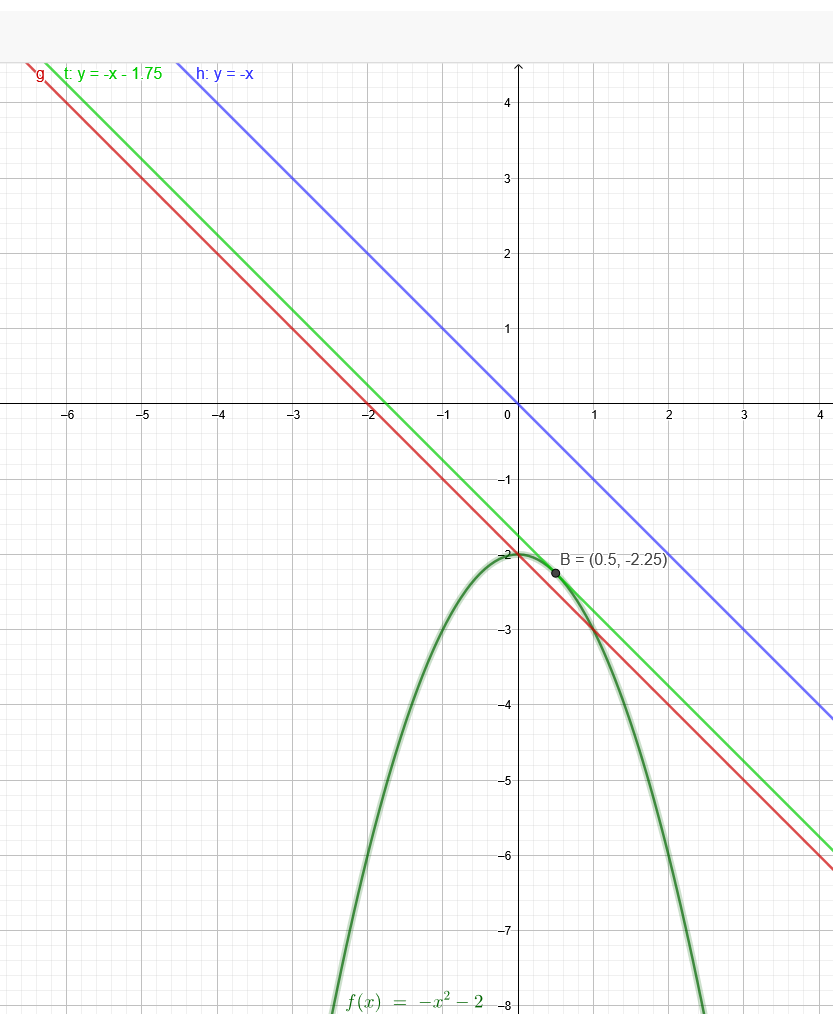
"In welchem Punkt P(x₀|f(x₀)) ist die Tangente an den Graphen von f parallel zur Geraden g mit g(x)=−x−2

f(x)=−x²−2"

Ich zeige nun einen Weg ohne Ableitung:

g(x)=−x−2 hat eine Steigung von m=-1 . Da nun diese Gerade die Parabel in 2 Punkten schneidet verändere ich g(x)=−x−2 in h(x)=-x . Nun setze ich f(x)=h(x) :

−x²−2=-x  → x²+2=x →  x²-1x=-2  → (x-\( \frac{1}{2} \) )^2=-\( \frac{7}{4} \) =\( \frac{7}{4} \) *\( i^{2} \)

x₁=\( \frac{1}{2} \)+\( \frac{i}{2} \)•\( \sqrt{7} \)

x₂=\( \frac{1}{2} \)-\( \frac{i}{2} \)•\( \sqrt{7} \)

Somit liegt der Berührpunkt bei B(\( \frac{1}{2} \)| f (  \( \frac{1}{2} \)  ))